【技術解説】集合の類似度(Jaccard係数，Dice係数，Simpson係数)

執筆：金子冴

前回の記事(【技術解説】似ている文字列がわかる！レーベンシュタイン距離とジャロ・ウィンクラー距離の計算方法とは)では，文字列同士の類似度(距離)が計算できる手法を紹介した．また，その記事の中で，自然言語処理分野では主に文書，文字列，集合等について類似度を計算する場面が多いことについても触れた．今回は集合同士の類似度を表現する以下の３つの係数と計算方法について解説する．
●Jaccard係数
●Dice係数
●Simpson係数

その前に，自然言語処理で類似度を表す指標について確認しよう．

自然言語処理で使用される類似度(距離)

自然言語処理の分野では，類似度を測る対象によって手法を使い分ける．
ここでは事前に，主に使用される手法について確認しておこう．

ベクトル同士の類似度

　●コサイン類似度
　●ピアソンの相関係数
　●偏差パターン類似度

集合同士の類似度(今回の解説対象)

　●Jaccard係数
　●Dice係数
　●Simpson係数

文字列同士の類似度

　●ハミング距離
　●レーベンシュタイン距離
　●ジャロ・ウィンクラー距離
　※レーベンシュタイン距離，ジャロ・ウィンクラー距離については，以下の記事で解説済み．
　　文字列の類似度(Levenshtein距離，jaro-winkler距離)

それでは本題の集合同士の類似度について，Jaccard係数から確認していこう．

Jaccard係数(Jaccard index)とは

Jaccard係数の定義と意味

Jaccard係数は，「Jaccard index」や「Jaccard similarity coefficient」と呼ばれる．
ある集合Aと別の集合BについてのJaccard係数J(A,B)は，以下の式で定義される．
（集合Aと集合Bがどちらも空集合$\phi$の時，J(A,B)＝1とする）
$$J(A,B)=\frac{|A \cap B|}{|A \cup B|}$$
わかりやすく，図を用いると以下のようになる．

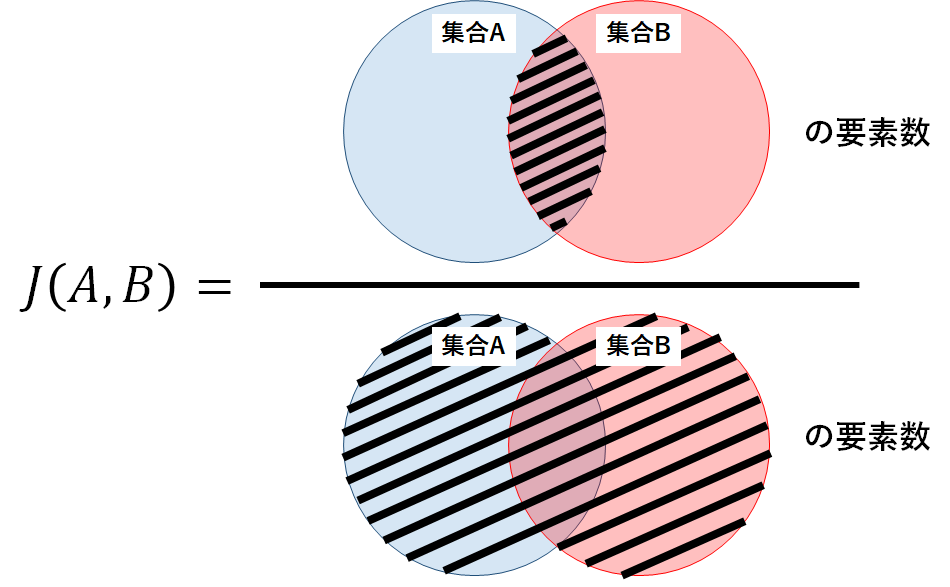
上記の定義より，Jaccard係数は2つの集合に含まれている要素のうち共通要素が占める割合を表しており，係数は0から1の間の値となることがわかる．Jaccard係数が大きいほど2つの集合の類似度は高い(よく似ている)といえる．

Jaccard係数の計算アルゴリズムおよびpython実装方法

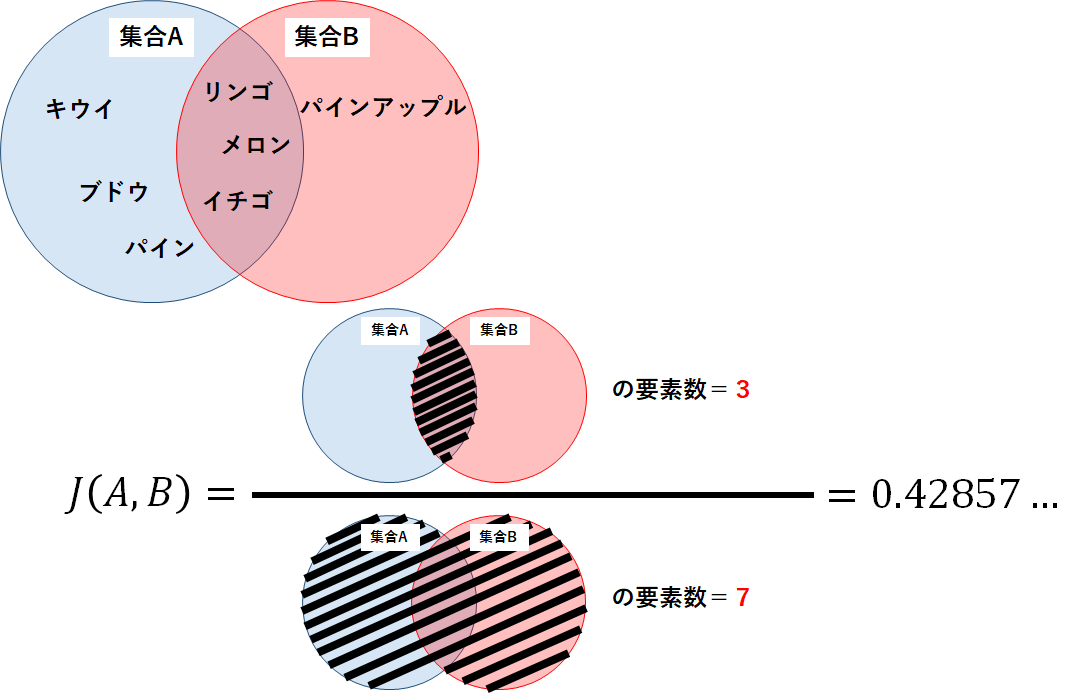
今回は例として，以下の集合Aと集合Bを用いてJaccard係数の計算アルゴリズムと実装方法を確認しよう．
集合A=[“リンゴ”,”ブドウ”,”イチゴ”,”パイン”,”キウイ”,”メロン”]
集合B=[“メロン”,”イチゴ”,”リンゴ”,”パインアップル”]
実装したソースコードは以下のようになる．計算の結果，集合Aと集合BのJaccard係数は約0.429となった．

#Jaccard係数(overlap coefficiant)の計算アルゴリズム
def jaccard_similarity_coefficient(list_a,list_b):
    #集合Aと集合Bの積集合(set型)を作成
    set_intersection = set.intersection(set(list_a), set(list_b))
    #集合Aと集合Bの積集合の要素数を取得
    num_intersection = len(set_intersection)

    #集合Aと集合Bの和集合(set型)を作成
    set_union = set.union(set(list_a), set(list_b))
    #集合Aと集合Bの和集合の要素数を取得
    num_union = len(set_union)

    #積集合の要素数を和集合の要素数で割って
    #Jaccard係数を算出
    try:
        return float(num_intersection) / num_union
    except ZeroDivisionError:
        return 1.0	

if __name__== '__main__':
    list_a = ["リンゴ","ブドウ","イチゴ","パイン","キウイ","メロン"]	#集合A
    list_b = ["メロン","イチゴ","リンゴ","パインアップル"]		#集合B

    jaccard = jaccard_similarity_coefficient(list_a,list_b)	#Jaccard係数を計算
    print(jaccard)	#計算結果を出力　⇒　0.42857142857142855

#Jaccard係数(overlap coefficiant)の計算アルゴリズム

def jaccard_similarity_coefficient(list_a,list_b):

#集合Aと集合Bの積集合(set型)を作成

set_intersection = set.intersection(set(list_a), set(list_b))

#集合Aと集合Bの積集合の要素数を取得

num_intersection = len(set_intersection)

#集合Aと集合Bの和集合(set型)を作成

set_union = set.union(set(list_a), set(list_b))

#集合Aと集合Bの和集合の要素数を取得

num_union = len(set_union)

#積集合の要素数を和集合の要素数で割って

#Jaccard係数を算出

try:

return float(num_intersection) / num_union

except ZeroDivisionError:

return 1.0

if __name__== '__main__':

list_a = ["リンゴ","ブドウ","イチゴ","パイン","キウイ","メロン"] #集合A

list_b = ["メロン","イチゴ","リンゴ","パインアップル"] #集合B

jaccard = jaccard_similarity_coefficient(list_a,list_b) #Jaccard係数を計算

print(jaccard) #計算結果を出力　⇒　0.42857142857142855

念のため，定義式から手計算してみよう．
以下の図が計算の過程と結果であり，プログラムの結果と一致することがわかる．

Jaccard係数の欠点

Jaccard係数では分母に2つの集合の和集合を採用することで値を標準化し，他の集合同士の類似度に対する絶対評価を可能にしている．しかし，Jaccard係数は2つの集合の差集合の要素数に大きく依存するため，差集合の要素数が多いほどJaccard係数は小さくなる．これは，人の目から判断した際の「共通要素が多いほど類似度が高い」という感覚と異なっている．

そこで，差集合の要素数の影響を抑え，共通要素の要素数の影響に重みをおくDice係数が提案された．
では次に，Dice係数の解説にうつろう．また，残り2つの係数(Dice係数，Simpson係数)については，Jaccard係数との関連も含めて解説していく．

Dice係数(Sørensen–Dice coefficient)とは

Dice係数の定義と意味

Dice係数は「Sørensen–Dice index」や「Sørensen–Dice coefficient」と呼ばれる．
ある集合Aと別の集合BについてのDice係数DSC(A,B)は，以下の式で定義される．
$$DSC(A,B)=\frac{2|A \cap B|}{|A|+|B|}$$
わかりやすく，図を用いると以下のようになる．

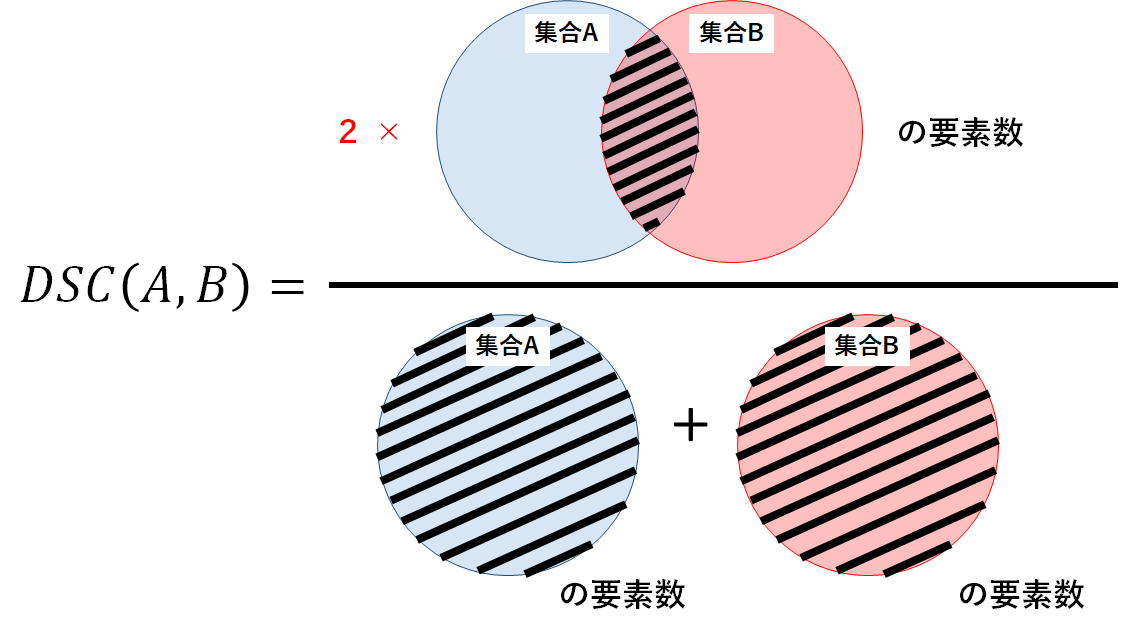
Dice係数の定義式は，Jaccard係数の定義式の分母$|A|\cup|B|$を$(|A|+|B|)/2$と変換することで得られる．よって，Dice係数は2つの集合の平均要素数と共通要素数の割合を表しており，Jaccard係数と同様に0から1の間の値となることがわかる．また，こちらもJaccard係数と同様にDice係数が大きいほど2つの集合の類似度は高い(よく似ている)といえる．

Jaccard係数とDice係数の関連

分母を「和集合の要素数」から「2集合の平均要素数」とすることで，一方の集合だけ要素数が膨大である場合などに類似度が著しく下がる問題を防ぎ，共通要素数を重視した類似度計算を実現している．

Dice係数の計算アルゴリズムおよびpython実装方法

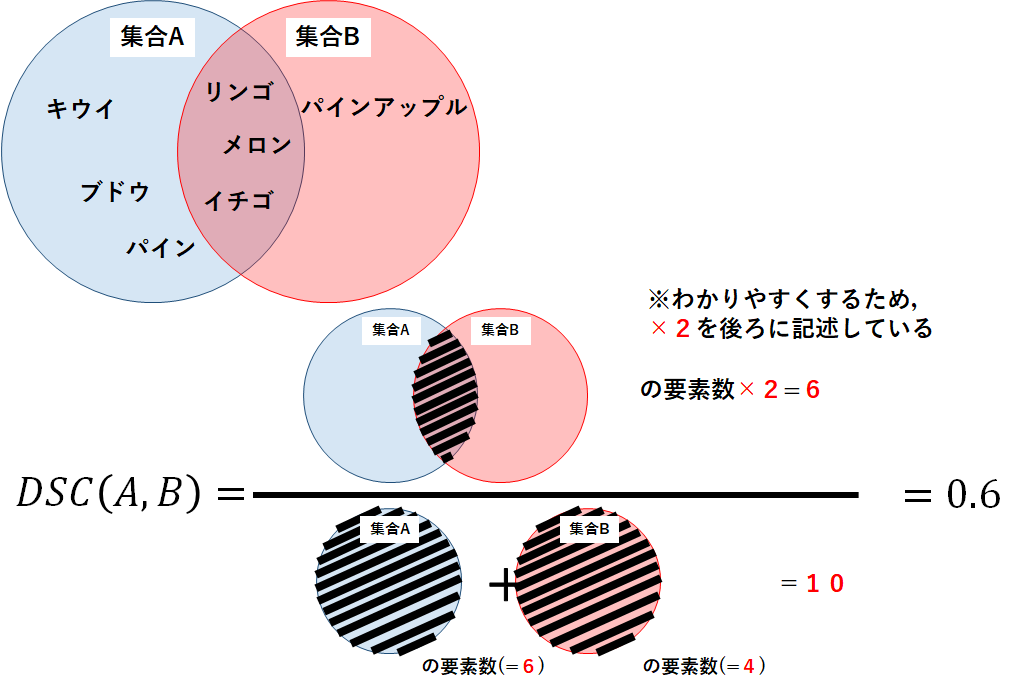
Jaccard係数の例を用いて，同様にDice係数の計算アルゴリズムと実装方法を確認しよう．
集合A=[“リンゴ”,”ブドウ”,”イチゴ”,”パイン”,”キウイ”,”メロン”]
集合B=[“メロン”,”イチゴ”,”リンゴ”,”パインアップル”]
実装したソースコードは以下のようになる．今回は集合Aと集合Bがどちらも空集合$\phi$の時，DSC(A,B)＝1.0とした．
計算の結果，集合Aと集合BのDice係数は0.6となり，Jaccard係数の計算値(約0.429)より高い結果となった．

#Dice係数の計算アルゴリズム
def dice_similarity_coefficient(list_a,list_b):
    #集合Aと集合Bの積集合(set型)を作成
    set_intersection = set.intersection(set(list_a), set(list_b))
    #集合Aと集合Bの積集合の要素数を取得
    num_intersection = len(set_intersection)

    #集合Aの要素数を取得
    num_listA = len(list_a)
    #集合Bの要素数を取得
    num_listB = len(list_b)

    #定義式に従い，Dice係数を算出
    try:
        return float(2.0 * num_intersection) / (num_listA + num_listB)
    except ZeroDivisionError:
        return 1.0	

if __name__== '__main__':
    list_a = ["リンゴ","ブドウ","イチゴ","パイン","キウイ","メロン"]	#集合A
    list_b = ["メロン","イチゴ","リンゴ","パインアップル"]		#集合B

    dsc = dice_similarity_coefficient(list_a,list_b)	#Dice係数を計算
    print(dsc)	#計算結果を出力　⇒　0.6

#Dice係数の計算アルゴリズム

def dice_similarity_coefficient(list_a,list_b):

#集合Aと集合Bの積集合(set型)を作成

set_intersection = set.intersection(set(list_a), set(list_b))

#集合Aと集合Bの積集合の要素数を取得

num_intersection = len(set_intersection)

#集合Aの要素数を取得

num_listA = len(list_a)

#集合Bの要素数を取得

num_listB = len(list_b)

#定義式に従い，Dice係数を算出

try:

return float(2.0 * num_intersection) / (num_listA + num_listB)

except ZeroDivisionError:

return 1.0

if __name__== '__main__':

list_a = ["リンゴ","ブドウ","イチゴ","パイン","キウイ","メロン"] #集合A

list_b = ["メロン","イチゴ","リンゴ","パインアップル"] #集合B

dsc = dice_similarity_coefficient(list_a,list_b) #Dice係数を計算

print(dsc) #計算結果を出力　⇒　0.6

念のため，定義式から手計算してみよう．
以下の図が計算の過程と結果であり，プログラムの結果と一致することがわかる．

Dice係数の欠点

『Jaccard係数とDice係数の関連』の項でも説明した通り，Dice係数の定義式は，Jaccard係数の定義式の分母を「和集合の要素数」から「2集合の平均要素数」とすることで，差集合の要素数が膨大になった場合に類似度への影響を緩和している．しかし，緩和しているとはいっても，2集合の要素数に大きな差があり差集合の要素数が膨大になった場合(例えば，一方の集合が別の集合を内包している等の場合)に，Dice係数は低下してしまう．

そこで，差集合の要素数の影響を極限まで抑えたSimpson係数が提案された．
次は，Simpson係数について，Jaccard係数との関連も含めて解説していく．

Simpson係数(Overlap coefficient)とは

Simpson係数の定義と意味

Simpson係数は「Overlap coefficient」や「Szymkiewicz–Simpson coefficient」と呼ばれる．
ある集合Aと別の集合BについてのSimpson係数overlap(A,B)は，以下の式で定義される．
$$overlap(A,B)=\frac{|A \cap B|}{\min\{|A|,|B|\}}$$
わかりやすく，図を用いると以下のようになる．

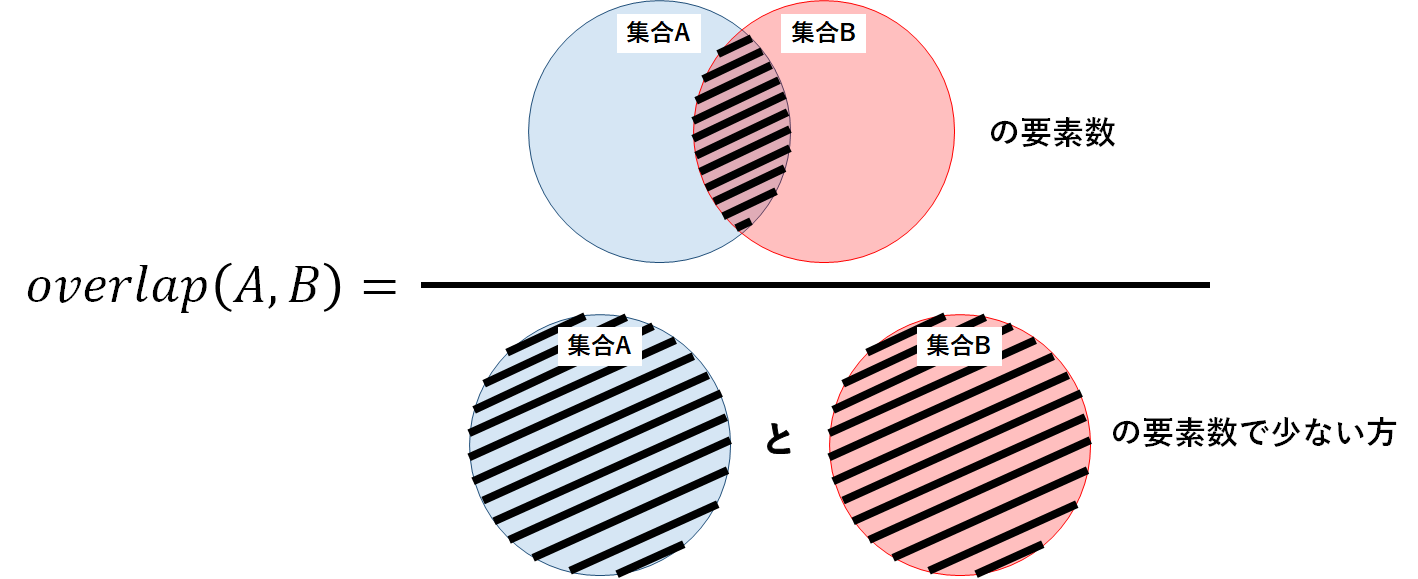
上記の定義より，Simpson係数は2つの集合のうち要素数が少ない方の要素数と共通要素数の割合を表しており，Jaccard係数やDice係数と同様に0から1の間の値となることがわかる．また，Simpson係数が大きいほど2つの集合の類似度は高い(よく似ている)といえる．

Jaccard係数とDice係数，Simpsonの関連

Dice係数の定義式は，Jaccard係数の定義式の分母$|A|\cup|B|$を$(|A|+|B|)/2$と変換することで得られた．これに対してSimpson係数の定義式は，Dice係数の定義式の分母を「2集合の平均要素数」から「2集合のうち少ない方の要素数」とすることで，Dice係数よりも差集合の要素数による影響を下げ，相対的に共通要素数を重視した類似度計算を実現している．

Simpson係数の計算アルゴリズムおよびpython実装方法

Jaccard係数，Dice係数の例を用いて，同様にSimpson係数の計算アルゴリズムと実装方法を確認しよう．
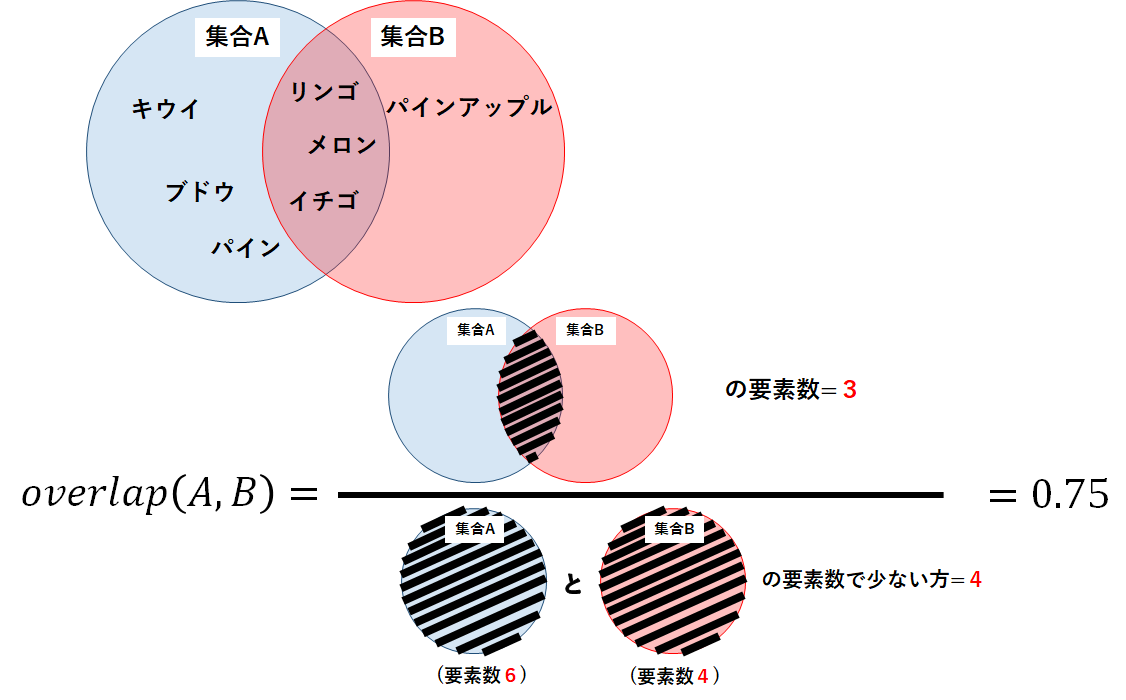
集合A=[“リンゴ”,”ブドウ”,”イチゴ”,”パイン”,”キウイ”,”メロン”]
集合B=[“メロン”,”イチゴ”,”リンゴ”,”パインアップル”]
実装したソースコードは以下のようになる．今回は集合Aと集合Bがどちらも空集合$\phi$の時，overlap(A,B)＝1.0とした．計算の結果，集合Aと集合BのSimpson係数は約0.75となった．

#Simpson係数(overlap coefficiant)の計算アルゴリズム
def overlap_coefficient(list_a,list_b):
    #集合Aと集合Bの積集合(set型)を作成
    set_intersection = set.intersection(set(list_a), set(list_b))
    #集合Aと集合Bの積集合の要素数を取得
    num_intersection = len(set_intersection)

    #集合Aの要素数を取得
    num_listA = len(list_a)
    #集合Bの要素数を取得
    num_listB = len(list_b)

    #定義式に従い，Simpson係数を算出
    try:
        return float(num_intersection) / min([num_listA,num_listB])
    except ZeroDivisionError:
        return 1.0	

if __name__== '__main__':
    list_a = ["リンゴ","ブドウ","イチゴ","パイン","キウイ","メロン"]	#集合A
    list_b = ["メロン","イチゴ","リンゴ","パインアップル"]		#集合B

    overlap = overlap_coefficient(list_a,list_b)	#Simpson係数を計算
    print(overlap)	#計算結果を出力　⇒　0.75

#Simpson係数(overlap coefficiant)の計算アルゴリズム

def overlap_coefficient(list_a,list_b):

#集合Aと集合Bの積集合(set型)を作成

set_intersection = set.intersection(set(list_a), set(list_b))

#集合Aと集合Bの積集合の要素数を取得

num_intersection = len(set_intersection)

#集合Aの要素数を取得

num_listA = len(list_a)

#集合Bの要素数を取得

num_listB = len(list_b)

#定義式に従い，Simpson係数を算出

try:

return float(num_intersection) / min([num_listA,num_listB])

except ZeroDivisionError:

return 1.0

if __name__== '__main__':

list_a = ["リンゴ","ブドウ","イチゴ","パイン","キウイ","メロン"] #集合A

list_b = ["メロン","イチゴ","リンゴ","パインアップル"] #集合B

overlap = overlap_coefficient(list_a,list_b) #Simpson係数を計算

print(overlap) #計算結果を出力　⇒　0.75

念のため，定義式から手計算してみよう．
以下の図が計算の過程と結果であり，プログラムの結果と一致することがわかる．

Simpson係数の欠点

『Jaccard係数とDice係数，Simpsonの関連』の項でも説明した通り，Simpson係数の定義式は，Dice係数の定義式の分母を「2集合の平均要素数」から「2集合のうち少ない方の要素数」とすることで，Dice係数よりも差集合の要素数による影響を下げ，相対的に共通要素数を重視した類似度計算を実現している．しかし，Simpson係数では要素数が少ない方の要素数を分母としているため，一方の集合の要素数が少ない場合に，差集合の要素数がどれだけ多くても類似度がほぼ1となってしまう．
この問題を解決するためには，2つの集合の要素数に条件(閾値を設定する，2集合間の要素数の差が範囲内である等)を付加するとよい．

また，一方の集合が別の集合の真部分集合の場合に，Jaccard係数(もしくはDice係数)とSimpson係数では値が異なるため，使用する場面に応じて使い分ける必要がある．次の項では，Jaccard係数，Dice係数，Simpson係数の使い分けについて，例を用いて確認しよう．

Jaccard係数，Dice係数，Simpson係数の使い分けと判断基準

ここまでの説明で，Jaccard係数を拡張したものがDice係数，Dice係数を拡張したものがSimpson係数であることはご理解いただけただろう．この説明では，Simpson係数が最も優れているようにとらえることもできるが，使用する場面によってはそうとは限らない．ここでは，いくつかのパターンを用いてそれぞれの係数を使い分ける方法を確認する．

パターン１：2集合の一部が共通要素

初めに，各係数の解説でも使用したような，2集合の一部が共通要素である場合を考えよう．
図で表すと，以下のようになる．

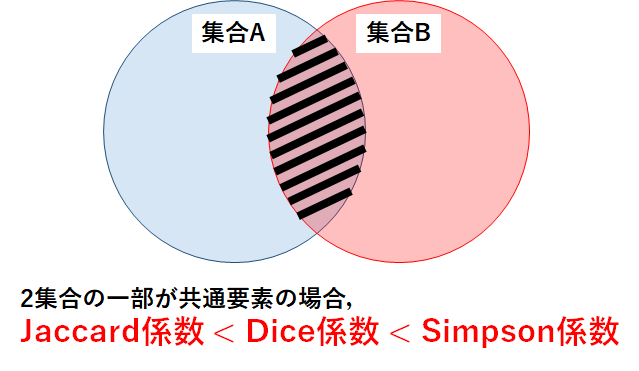
この場合，Jaccard係数よりDice係数の方が，さらにDice係数よりSimpson係数の方が差集合の影響を抑えているため，各係数の値はJaccard係数 < Dice係数 < Simpson係数となる．

パターン２：2集合に共通要素がない

次に，2集合に共通要素がない，つまり$A \cap B = \phi$の場合を考える．
図で表すと，以下のようになる．

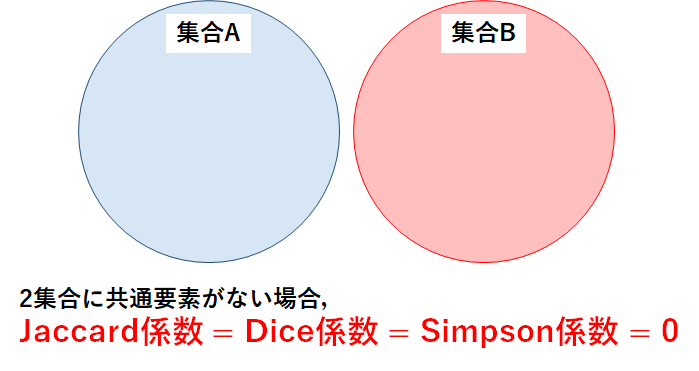
各係数の分子には，共通要素の数を表す$|A \cap B|$の項がある．共通要素がない場合は当然$|A \cap B| = 0$のため，Jaccard係数 = Dice係数 = Simpson係数 = 0となる．

パターン３：一方の集合が別の集合の真部分集合

最後に，一方の集合が別の集合の真部分集合である場合を考えよう．
実は，各係数の使い分けにおいて最も重要となるのがこのパターンである．
図で表すと，以下のようになる．

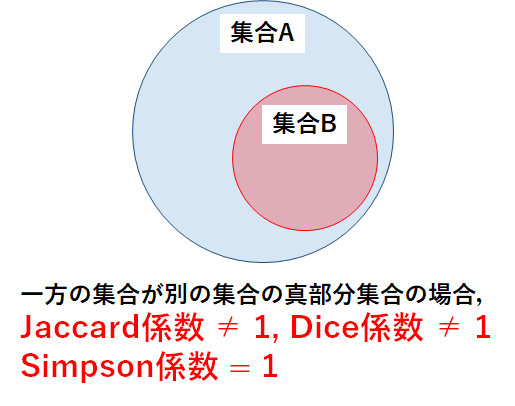
この場合のJaccard係数とDice係数の値は1にはならない．Jaccard係数とDice係数では差集合の影響を受けるため，真部分集合の場合でも完全に一致しているとは判断されない．しかし，Simpson係数では値が1になる．真部分集合の場合，「要素数の少ない方(集合B)の要素数=共通要素の要素数」が成り立つためである．
このように，一方の集合が別の集合の部分集合である場合に，Jaccard係数およびDice係数とSimpson係数では考え方に大きな違いが生まれる．自分が使用する際には真部分集合をどのように考慮するのかをベースに，どの係数計算を採用すべきかを考える必要がある．

最後に，Jaccard係数，Dice係数，Simpson係数の応用可能性について確認しよう．

Jaccard係数，Dice係数，Simpson係数の応用可能性

今回解説した３つの係数は，最初に確認した通り，いずれも集合同士の類似度を表す指標である．
集合同士の類似度がわかると以下のようなことに応用できる．
●文書同士の類似度計算
　⇒文書を「単語の集合」ととらえることで，集合の類似度=文書の類似度と置き換えることができる．
●トピック同士の関連推定
　⇒トピック毎の単語の集合を作成して類似度を計算すると，その値はトピック同士の類似度と言い換えることができるだろう．これにより，あるトピックの話題が出現したときに別のトピックと関連付けるべきかどうかを判断する目安が得られる．
●文字列同士の共起推定
　⇒トピック同士の関連推定に関係して，「あるトピックの単語が出現した際に，類似度の高いトピックの単語も出現するかもしれない」という推定ができるようになる．

参考

・Jaccard index – wikipedia
・Sørensen–Dice coefficient – wikipedia
・Overlap coefficient – wikipedia
・A SURVEY ON SIMILARITY MEASURES IN TEXT MINING
・文書の類似度計算（Python3.5）：Jaccard係数，Dice係数，Simpson係数
・Jaccard係数、Dice係数、Simpson係数

人工知能・機械学習・自然言語処理周辺の技術情報

自然言語処理で使用される類似度(距離)

ベクトル同士の類似度

集合同士の類似度(今回の解説対象)

文字列同士の類似度

Jaccard係数(Jaccard index)とは

Jaccard係数の定義と意味

Jaccard係数の計算アルゴリズムおよびpython実装方法

Jaccard係数の欠点

Dice係数(Sørensen–Dice coefficient)とは

Dice係数の定義と意味

Jaccard係数とDice係数の関連

Dice係数の計算アルゴリズムおよびpython実装方法

Dice係数の欠点

Simpson係数(Overlap coefficient)とは

Simpson係数の定義と意味

Jaccard係数とDice係数，Simpsonの関連

Simpson係数の計算アルゴリズムおよびpython実装方法

Simpson係数の欠点

Jaccard係数，Dice係数，Simpson係数の使い分けと判断基準

Jaccard係数，Dice係数，Simpson係数の応用可能性

参考

関連記事はこちら