執筆:金子冴
人はだれしも間違いを犯すものである.徹夜で仕上げた報告書を提出した後,よく見直してみると誤字脱字が山ほど見つかった経験が読者にもあるだろう(もしかすると私だけかもしれないが).そういう時,もし自動で間違っている単語を見つけてくれるプログラムがあったら…と考える人もいるかもしれない.そこで今回は,文字列同士の似ている度合いを計算する2つの手法を紹介しよう.
●レーベンシュタイン距離(Levenshtein Distance)
●ジャロ・ウィンクラー距離(Jaro-winkler Distance)
目次
文字列の類似度,距離
編集処理(挿入,削除,置換)
レーベンシュタイン距離(Levenshtein Distance)とは
ジャロ・ウィンクラー距離(Jaro-winkler Distance)とは
レーベルシュタイン距離とジャロ・ウィンクラー距離の応用可能性
参考
文字列の類似度,距離
初めに類似度というものを理解しよう.類似度とは,2つの対象が似ている度合いを表す尺度である.対象は何でもよく,自然言語処理分野では主に文書,文字列,集合等について類似度を計算する場面が多いように見受けられる.また,今回紹介する手法を見たときに「なんで距離なんだ?」と思った読者も少なくないであろう.自然言語処理分野では,類似度のことを距離と呼ぶ場面がしばしば見られる.類似度と距離の関係は以下のようになる.類似度と距離では値の大小が逆になるため,注意が必要である.
・2対象が似ている = 類似度が高い = 距離が近い(値が小さい)
・2対象が似ていない = 類似度が低い = 距離が遠い(値が大きい)
編集処理(挿入,削除,置換)
さて,今回紹介する2つの手法を理解するためには事前に編集処理というものを理解しておく必要がある.編集処理とは,ある文字列に対して「挿入(insertion)」,「削除(deletion)」,「置換(substitution)」の3つの操作を組み合わせ,別の文字列に変換する処理を指す.それぞれの操作について,図を交えて解説していこう.
・挿入(insertion)
「挿入」は,文字列に文字を1つ入れる操作である.追加する位置はどこでもよい.例えば,「かんり(管理)」の3文字目(「ん」の後)に「き」を挿入すれば「かんきり(缶切り)」になるし,「コップ」の先頭に「ス」を挿入すれば「スコップ」になる.ただし,追加する文字は1回につき1文字でなければならない.例えば,「たんし(端子)」を「たんぱくしつ(タンパク質)」にするためには3文字挿入する必要があるが,一度に3文字は挿入できないため,「ぱ」の挿入に1回,「く」の挿入に1回,「つ」の挿入に1回,合計3回の挿入操作が必要となる.
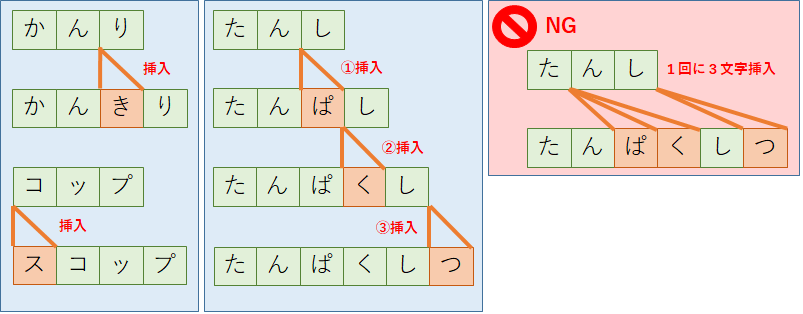
・削除(deletion)
「削除」は,文字列の文字を1つ消す操作である.消す位置はどこでもよい.挿入で用いた例を用いて説明すると,「かんきり(缶切り)」の3文字目を削除すれば「かんり(管理)」になるし,「スコップ」の1文字目を削除すれば「コップ」になる.また,「挿入」操作と同様に,削除する文字は1回につき1文字でなければならない.
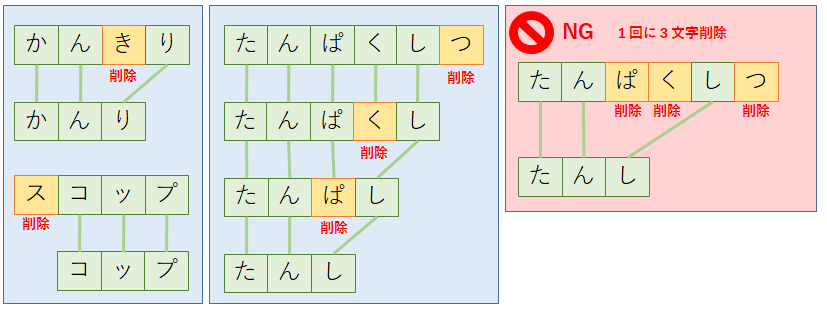
・置換(substitution)
「置換」は,文字列の文字を1つ別の文字に変える操作である.例えば,「たいこ(太鼓)」の3文字目を「や」に置換すると「たいや(タイヤ)」になり,「テスト」の2文字目を「ン」に置換すると「テント」になる.「挿入」操作,「削除」操作のときと同じく,置換する文字は1回につき1文字でなければならない(図解中の説明は割愛).また,置換操作は1文字削除⇒1文字挿入でも再現可能であるため,「挿入」と「削除」のみを「編集」処理に採用して距離を計算する場合もある.
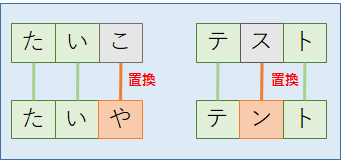
それでは,編集処理について理解できたところで,まずはレーベンシュタイン距離について解説する.
レーベンシュタイン距離(Levenshtein Distance)とは
まずはレーベンシュタイン距離の意味と計算方法について確認しよう.
レーベンシュタイン距離の意味と計算方法
レーベンシュタイン距離の意味
レーベンシュタイン距離(Levenshtein Distance)は,ある文字列と別の文字列の最小編集距離で表される距離である.なお,計算方法の項目で再度解説するが,編集操作ごとに異なるコストを指定してもよい.そのため,「編集距離が最小である=レーベンシュタイン距離である」と断定することはできないため注意が必要である.
レーベンシュタイン距離の計算方法
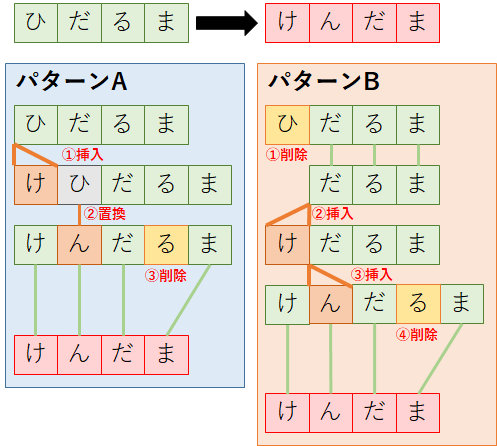
例として,「ひだるま」(以下,s1)を「けんだま」(以下,s2)に変換する際のレーベンシュタイン距離を計算してみよう.
s1をs2に変換する編集パターンはいくつかあるが,その中で以下の2つのパターン(パターンA,B)をピックアップする.なお,今回はs1をs2に変換する場合を考える.
【パターンA:編集回数3回】
①1文字目に「け」を挿入する.
②2文字目の「ひ」を「ん」に置換する.
③4文字目の「る」を削除する.
【パターンB:編集回数4回】
①1文字目の「ひ」を削除する.
②1文字目に「け」を挿入する.
③2文字目に「ん」を挿入する.
④4文字目の「る」を削除する.
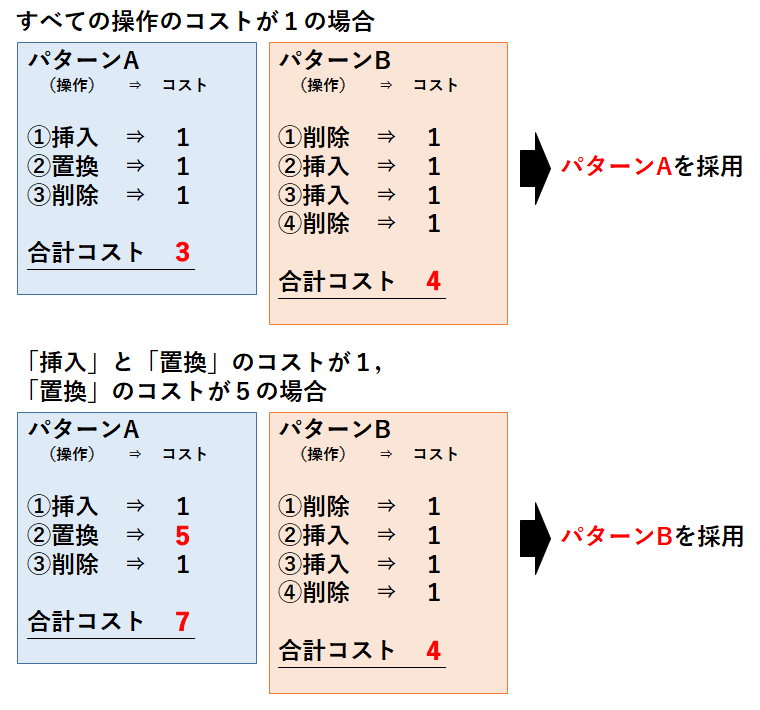
編集のパターンが洗い出せたところで,次は編集操作のコストについて考えよう.前述のとおり,レーベンシュタイン距離を考える際には「挿入」,「削除」,「置換」のコストに別々の値を割り振ることもできる.単純に3つの操作のコストをすべて1としてもよいし,例えば,「挿入」「削除」はコスト1,「置換」だけコスト5にすることも可能である.先ほど挙げた,「ひだるま」を「けんだま」に変換するパターンを用いて考えてみよう.
編集コストがすべて1の場合
それぞれのパターンの編集コストは編集回数と等しくなるため,パターンAの編集距離は3,パターンBの編集距離は4となる.レーベンシュタイン距離(最小編集距離)は3となる.
編集コストが操作ごとに異なる場合
例えば,「挿入」「削除」をコスト1,「置換」をコスト5としよう.それぞれのパターンの編集距離を確認すると,パターンAが7,パターンBが4となる.この場合,レーベンシュタイン距離(最小編集距離)は4となる.
このように,編集回数だけではレーベンシュタイン距離かどうかを判断することはできないため,注意する必要がある.
補足:レーベンシュタイン距離の拡張
今回紹介したレーベンシュタイン距離には,欠点がある.例を挙げて解説しよう.
「カラクリ」と「ボンゴレ」という2つの文字列について,編集コストがすべて1である場合のレーベンシュタイン距離は4である.同様に「テスト」と「テストパターン」という2つの文字列について計算すると,レーベンシュタイン距離は同じく4になる.人の目から見ると後者の方が文字列が似ていると判断できるが,レーベンシュタイン距離は同じであるため,前者と後者は同じ類似度であると判断されてしまう.
このような実感との齟齬を防ぐためには「標準化」という処理をするとよい.例えば,文字列で標準化するとどうなるだろうか.前者の「カラクリ」と「ボンゴレ」の距離4を,2つの文字列の長さ4で割ると,標準化後のレーベンシュタイン距離は1となる.次に,後者の「テスト」と「テストパターン」の距離4を,2つの文字列のうち長い方の文字列の長さ7で割ると,標準化後のレーベンシュタイン距離は約0.57となり,後者の方が類似度が高いという結果を得ることができる.
このように,標準化されたレーベンシュタイン距離(Normalized Levenshtein Distance)を用いることで,実感に近い結果を得られる場合がある.標準化は類似度以外の計算時にも重要になってくるため,新たな手法を用いる際は定義と合わせて理解しておくと良い.
以上が,レーベンシュタイン距離の説明である.では次に,ジャロ・ウィンクラー距離について解説しよう.
ジャロ・ウィンクラー距離(Jaro-winkler Distance)とは
では,ジャロ・ウィンクラー距離の意味と計算方法について確認しよう.
ジャロ・ウィンクラー距離の意味と計算方法
ジャロ・ウィンクラー距離の意味
ジャロ・ウィンクラー距離(Jaro-winkler Distance)は,ある文字列と別の文字列で一致する文字数と置換の要不要から距離を計算する.ジャロ・ウィンクラー距離は,距離の取りうる値が0~1であり,距離の数値が大きいほど文字列間の類似度が高いことを表す.そのため,距離が0の時は全く異なる文字列であることを,距離が1の時は完全に一致している文字列であるという意味になる.
ジャロ・ウィンクラー距離の計算方法
ジャロ・ウィンクラー距離を計算するためには,まずJaro Distanceを計算する必要がある.
Jaro Distanceの計算
Jaro Distance Φの定義式は以下のとおりである.ただし,c=0の時,Φ=0である.
W1,W2,W3について
W1は2つの文字列のうち1つ目の文字列の重み,W2は2つ目の文字列の重み,Wtはs1をs2に置換する際にかかる重みを調整するための定数であり,W1=W2=Wt=1/3とするのが一般的である.
d,rについて
dはs1の長さ,rはs2の長さである.
c,τについて
cはs1とs2のある区間内で一致する文字数である.具体的には,2つの文字位置が以下の式で算出される値より離れていない場合にカウントする.
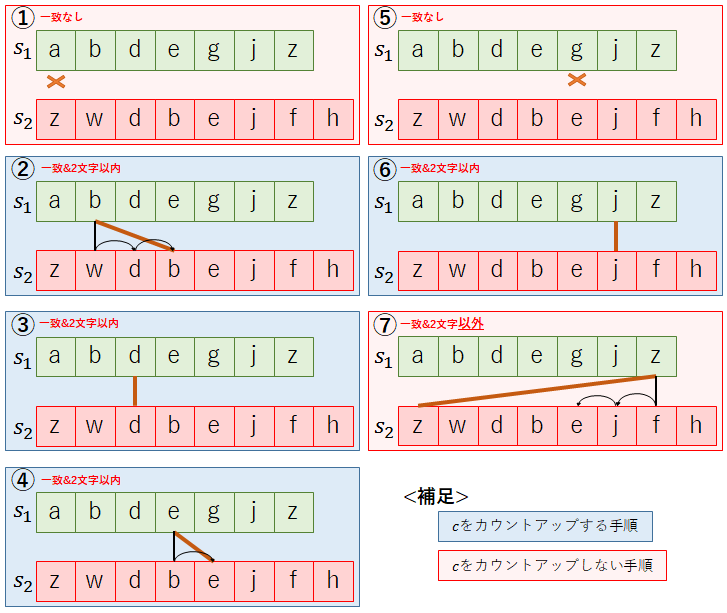
簡単な例を用いてcとτの計算方法を確認しよう.s1=”abdegjz”,s2=”zwdbejfh”の場合,cはいくつになるだろうか.始めに,区間を決定するための値を計算しよう.
次に,s1とs2を比較し,一致する文字のうち3文字以上離れていない(2文字以内の)文字数をカウントする.
①s1:1文字目「a」⇒s2:一致なし⇒c=0(カウントなし)
②s1:2文字目「b」⇒s2:4文字目,かつ2文字以内⇒c=1(カウントアップ)
③s1:3文字目「d」⇒s2:3文字目,かつ2文字以内⇒c=2(カウントアップ)
④s1:4文字目「e」⇒s2:5文字目,かつ2文字以内⇒c=3(カウントアップ)
⑤s1:5文字目「g」⇒s2:一致なし⇒c=3(カウントなし)
⑥s1:6文字目「j」⇒s2:6文字目,かつ2文字以内⇒c=4(カウントアップ)
⑦s1:7文字目「z」⇒s2:1文字目,2文字以外のためカウントなし⇒c=4(カウントなし)
よって,c=4となる.
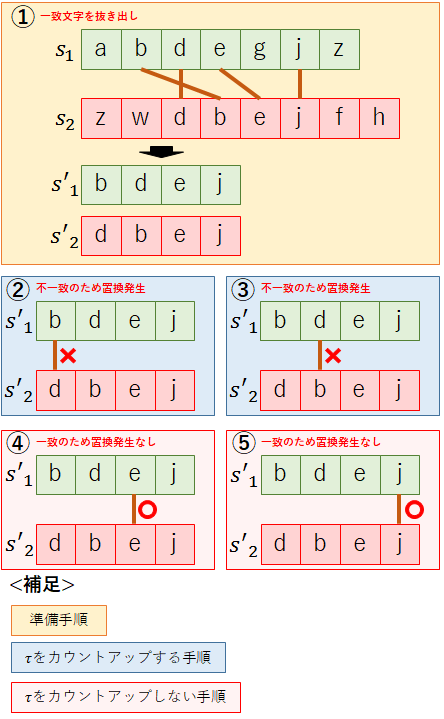
τは,s1をs2に編集する際に,置換が必要な文字数を2で割った数値である.置換が必要な文字数はs1とs2で一致する文字を順に抜き出し,各文字を比較することで計算する.先ほどと同様,s1=”abdegjz”,s2=”zewbdjfh”の例を用いて,τを計算しよう.
①まず,s1とs2の一致する文字を順に抜き出し,s’1とs’2とおく.
s’1=”bdej”
s’2=”dbej”
②s’1とs’2の1文字目を比較し,一致しているかを確認する.
今回の例ではs’1:「b」,s’2:「d」で一致していないため,置換が発生する.
③s’1とs’2の2文字目を比較し,一致しているかを確認する.
今回の例ではs’1:「d」,s’2:「b」で一致していないため,置換が発生する.
③s’1とs’2の3文字目を比較し,一致しているかを確認する.
今回の例ではs’1:「e」,s’2:「e」で一致していないため,置換は発生しない.
④s’1とs’2の4文字目を比較し,一致しているかを確認する.
今回の例ではs’1:「j」,s’2:「j」で一致していないため,置換は発生しない.
以上から,s’1を2回置換すればs’2になるため,τ=2/2=1となる.
Jaro Distanceを算出した後,そこからジャロ・ウィンクラー距離を計算する.
ジャロ・ウィンクラー距離の計算
ジャロ・ウィンクラー距離Φnは以下の式で定義される.
上記の式中のiを,s1とs2の先頭から比較して一致している文字数(最大でi=4)に設定して計算すると,s1とs2のジャロ・ウィンクラー距離が算出できる.念のため,iの設定方法について確認する.例えばs1=”John”,s2=”Johhhn”とした場合,s1とs2の3文字目までの”Joh”は一致しているため,i=3とする.
(補足)
ジャロ・ウィンクラー距離は「人が打ち間違えた場合,先頭の何文字かは正しく入力されているはずだ」という考えのもとに編み出された手法である.英語圏では4文字程度の接頭語は珍しくないためiの範囲をi=1,2,3,4としているようだ(日本語の場合は3~4文字の接頭語はあまり見かけないため,i=1,2のようにiの範囲を狭めてもよいかもしれない).
以上が,ジャロ・ウィンクラー距離の説明である.
レーベルシュタイン距離とジャロ・ウィンクラー距離の応用可能性
レーベンシュタイン距離とジャロ・ウィンクラー距離は,どちらも文字列同士の類似度を数値化する手法であった.導入部分で述べた「自動で間違っている単語を見つけてくれるプログラム」にとって,文字列同士の類似度はとても重要な要素となる.例えば,あらゆる単語の情報を保持しているデータベースがあるとして,あるユーザが入力した文字列がそのデータベースに存在しなかった場合,入力された文字列が誤りであることはわかるだろう.しかし,プログラムによって自動で修正したり,「もしかして:〇〇」のようにレコメンドすることはできない.しかし,文字列同士の類似度がわかれば自動修正やレコメンド機能を容易に作成することができるようになるのだ.Google検索時に誤った文字列で検索してしまった場合の下図のようなレコメンドも,この文字列の類似度を応用した機能であろう.
参考
2つの文字列の類似度を数値化 レーベンシュタイン距離とジャロ・ウィンクラー距離の解説
・レーベンシュタイン距離
レーベンシュタイン距離 – wikipedia
文字列の類似度を測る(1) レーベンシュタイン距離
文字列の類似度を測る(3) レーベンシュタイン距離の拡張
・ジャロ・ウィンクラー距離
Jaro–Winkler distance – wikipedia
String Comparator Metrics and Enhanced Decision Rules in the Fellegi-Sunter Model of Record Linkage

