【技術解説】単語の重要度を測る？TF-IDFとOkapi BM25の計算方法とは

執筆：金子冴

世の中には単なるメモ書きから予算案，スポーツ記事や文学作品等，数えられないほどの文書が存在する．例えば，その数多の文書から「スポーツに関する記事が読みたい」と思った時，どれがスポーツに関する文書なのか判断する必要があるだろう．しかし，すべての文書を目で読んで判断することは到底不可能であり，現実的ではない．今回は，数多の文書に含まれる単語の重要度を測る手法であるTF-IDFとOkapi BM25について解説する．

TF-IDFとは

TF-IDFとは，文書内に出現する単語について，以下の２つの情報から，その単語の重要度を算出する手法である．
　・単語の出現頻度(TF値)
　・単語の逆文書頻度(IDF値)
それぞれについて，その値が表す意味と計算式を確認しよう．

TF(Term Frequency)値の意味と計算式

TF値の意味

TF値は文書内でのある単語の出現頻度である．すなわち，文書内のすべての単語の出現回数のうち，その単語の出現回数が占める割合を表す．この式から，出現回数が多いほどTF値は大きくなり，出現回数が低いほどTF値は小さくなることがわかるだろう．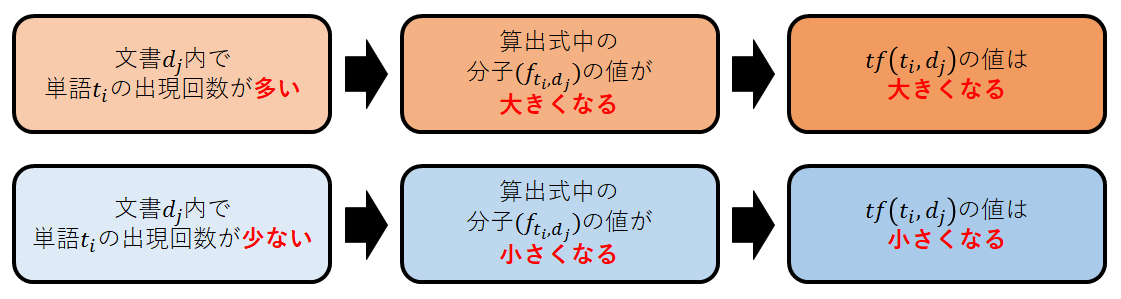

TF値の計算式

ある文書d_jに出現する単語t_iについて考える場合，出現回数を表す関数を$f$とするとTF値は以下の式から算出できる．TF値は文書ごと，単語ごとに存在するため，同じ単語であっても文書が異なる場合は，値が異なる可能性がある．

$$tf(t_i,d_j)=\frac{文書d_j内の単語t_iの出現回数}{文書d_jのすべての単語の出現回数の和}=\frac{f(t_i,d_j)}{\sum_{t_k\in d_j}f(t_k,d_j)}$$

ここまでの話から，単純に考えると文書内にたくさん出現している単語ほど，その文書をよく表しているといった印象を受けるがそうとは限らない．
例えば，「院長のお仕事」というトピックと，「看護師のお仕事」というトピックの２つの文書があった場合に，どちらの文書にも「病院」という単語が複数回出現するであろう．しかし，「病院」という単語では，それぞれの文書の特徴を表しているとは考えにくい．そこで重要となるのが，「その単語が他の文書には存在していない」ことを表すIDF値である．

IDF(Inverse Document Frequency)値の意味と計算式

IDF値の意味

IDF値は文書集合の中のある単語が含まれる文書の割合の逆数を表す．単語が他の文章にも多く出現しているほどIDF値は小さくなり，単語が他の文章にあまり出現していないほどIDF値は大きくなる．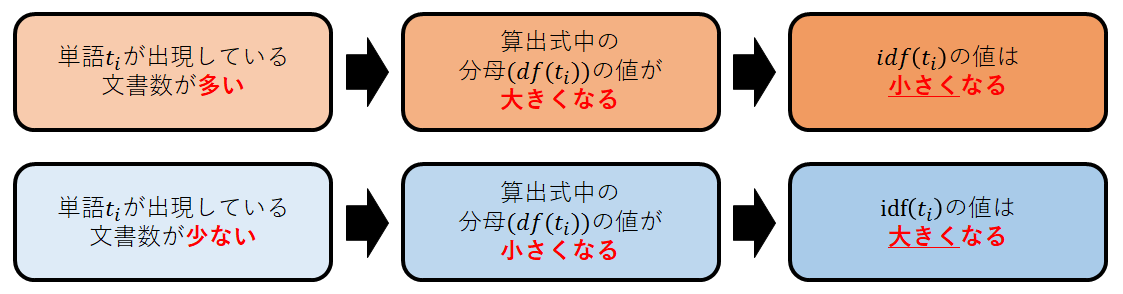

IDF値の計算式

ある文書集合における単語t_iについて考える場合，dfを単語t_iが出現する文書数とすると，IDF値は以下の式から算出できる．TF値と違い，IDF値は単語ごと存在することに注意が必要である．

$$idf(t_i)=\log{}\left(\frac{総文書数}{単語t_iが出現する文書数}\right)=\log{}\left(\frac{N}{df(t_i)}\right)$$

ただし，文書内に一度も出現しない単語のIDF値を計算しようとした場合，0除算(division-by-zero)が発生してしまう．そのため，分母に+1を追加した以下の式を使用するのが一般的である．

$$idf(t_i)=\log{}\left(\frac{総文書数}{単語t_iが出現する文書数+1}\right)=\log{}\left(\frac{N}{df(t_i)+1}\right)$$

さて，TF値とIDF値が算出できたところで，最後に単語毎の重要度を表すTF-IDF値の算出方法を確認しよう．

TF-IDF値の意味と計算式

TF-IDF値の意味

TF-IDF値はTF値とIDF値をかけ合わせて計算する．それにより，ある文書内での出現回数は多いが他の文書には出現していない単語のTF-IDF値は大きくなり，それ以外の単語についてはTF-IDF値は相対的に小さくなる．上記で算出したTF値とIDF値をかけ合わせることで，単語毎の重要度を算出することができる．TF-IDF値は文書ごと，単語ごとに存在する．

TF-IDF値の計算式

TF-IDF値は以下の式のように，TF値の計算式で計算した値とIDF値の計算式で計算した値をかけ合わせる．

$$tfidf(t_i,d_j)=tf(t_i,d_j)・idf(t_i)$$

次に，簡単な例を用いて手作業でTF-IDFによる単語の重み付けをしてみよう．

TF-IDFの計算例

２つの文書を例として考えよう．一方の文書Aを「リンゴとミカンとミカンとバナナ」，もう一方の文書Bを[バナナとミカンとイチゴとイチゴとブドウ]とする．今回の例では名詞のみを単語として考えることにする．

始めに，文書Aに出現する単語について，TF値を計算する．

$$tf(リンゴ,A)=\frac{1}{4}=0.25$$

$$tf(ミカン,A)=\frac{2}{4}=0.50$$

$$tf(バナナ,A)=\frac{1}{4}=0.25$$

同様に，文書Bに出現する単語についても，TF値を計算する．

$$tf(バナナ,B)=\frac{1}{5}=0.20$$

$$tf(ミカン,B)=\frac{1}{5}=0.20$$

$$tf(イチゴ,B)=\frac{2}{5}=0.40$$

$$tf(ブドウ,B)=\frac{1}{5}=0.20$$

次に，文書Aおよび文書Bに出現する単語について，IDF値を計算する．今回は0除算が発生しないことが事前にわかっているため，分母に+1を追加しない式を使用する．また，計算が簡単になるように対数の底は2とする(対数の底はなんでもよいが，一般的には2を取る場合が多い)．

$$idf(リンゴ)=\log{2}\left(\frac{2}{1}\right)=1.0$$

$$idf(ミカン)=\log{2}\left(\frac{2}{2}\right)=0.0$$

$$idf(バナナ)=\log{2}\left(\frac{2}{2}\right)=0.0$$

$$idf(イチゴ)=\log{2}\left(\frac{2}{1}\right)=1.0$$

$$idf(ブドウ)=\log{2}\left(\frac{2}{1}\right)=1.0$$

ここで，２文書ともに出現している「ミカン」と「バナナ」のIDF値が0.0となっていることに注目してほしい．この点については，後ほどTF-IDF値の計算時に再度確認する．

最後に，文書Aに出現する単語と文書Bに出現する単語について，TF-IDF値を計算し結果を比較しよう．まず，文書Aに出現する単語のTF-IDF値は以下のようになる．

$$tfidf(リンゴ,A)=tf(リンゴ,A)・idf(リンゴ)=0.25・1.0=0.25$$

$$tfidf(ミカン,A)=tf(ミカン,A)・idf(ミカン)=0.50・0.0=0.00$$

$$tfidf(バナナ,A)=tf(バナナ,A)・idf(バナナ)=0.25・0.0=0.00$$

ここで，２文書共に出現している「ミカン」と「バナナ」についてTF-IDF値が0.0になっているが，これはIDF値の計算時に確認したとおりIDF値が0.0となっている影響である．これは2文書ともに出現している単語（「ミカン」と「バナナ」）は，文書の特徴を表しているとはいえないと評価されたことを表している．
逆に「リンゴ」のTF-IDF値は0.25となっているため，文書Aにのみ出現している「リンゴ」は文書Aの他の単語(「ミカン」と「バナナ」)と比較して文書の特徴をよく表していると評価されたことがわかるだろう．
それでは同様に文書Bに出現する単語のTF-IDF値も計算してみよう．

$$tfidf(バナナ,B)=tf(バナナ,B)・idf(バナナ)=0.20・0.0=0.00$$

$$tfidf(ミカン,B)=tf(ミカン,B)・idf(ミカン)=0.20・0.0=0.00$$

$$tfidf(イチゴ,B)=tf(イチゴ,B)・idf(イチゴ)=0.40・1.0=0.40$$

$$tfidf(ブドウ,B)=tf(ブドウ,B)・idf(ブドウ)=0.20・1.0=0.20$$

文書Aと同様に，２文書共に出現している「ミカン」と「バナナ」についてはTF-IDF値が0.0になっているため，文書の特徴を表しているとはいえないと評価されている．
一方，「イチゴ」と「ブドウ」はどちらも文書Bにしか出現しないため，TF-IDF値は0.0より大きくなっている．ここで注目してほしいのは，「イチゴ」のTF-IDF値(0.40)と比べて，「ブドウ」のTF-IDF値(0.20)が低くなっている点である．これは一方にしか出現しない単語が複数ある場合，出現頻度が高い方が文書の特徴をよく表していると評価されたことを表している．
このように，TF-IDF値を計算することで文書に出現している単語のうち，どの単語が文書の特徴をよく表しているかが評価できる．

TF-IDFの欠点

TF-IDFの計算式では，文書に含まれる単語数が多いほどTF値が小さく，単語数が少ないほどTF値が大きくなる．これは，TF値の計算式の分母に「すべての単語の出現回数の和」をとっていることから明白であろう．そのため，複数の文書から重要度の高い単語を抽出して絶対評価でTF-IDF値を比較する場合，文書ごとの単語数の差による影響が大きく出てしまう．そこで，文書の単語数について標準化する項をTF-IDFに追加した手法であるOkapi BM25がStephen E.Robertson，Karen Spärck Jonesらによって提案された．

Okapi BM25とは

Okapi BM25はTF-IDFと同様に文書内に出現する単語についてその単語の重要度を算出する手法であり，一般的にTF-IDFより良い結果が得られるとされている．TF-IDFで使用した２つの情報(TF値，IDF値)に加え，文書に含まれる総単語数に関する情報（DL値）を用いる．
　・単語の出現頻度(TF値)
　・単語の逆文書頻度(IDF値)
　・文書の総単語数(DL値)
それぞれについて，その値が表す意味と計算式を確認しよう．先に述べておくが，IDF値の算出式がTF-IDFの場合と異なるため注意が必要である．

TF(Term Frequency)値の意味と計算式(Okapi BM25)

TF値についてはTF-IDFと同じ意味，計算式のため説明は割愛する．　⇒TF(Term Frequency)値の意味と計算式

IDF(Inverse Document Frequency)値の意味と計算式(Okapi BM25)

IDF値の意味(Okapi BM25)

TF-IDFと同じ意味のため説明は割愛する． ⇒IDF値の意味

IDF値の計算式(Okapi BM25)

TF-IDFと異なり，Okapi BM25の場合は以下の計算式を用いる．

$$idf(t_i)=\log{}\left(\frac{総文書数-単語t_iが出現する文書数+0.5}{単語t_iが出現する文書数+0.5}\right) \\ =\log{}\left(\frac{N-df(t_i)+0.5}{df(t_i)+0.5}\right)$$

TF-IDFの場合は0除算を回避するため分母に+1を追加した式を使用することが一般的と紹介したが，Okapi BM25の場合は定義式の段階で+0.5の項が追加されているため，0除算の考慮は不要である．

DL(Document Length)値の意味と計算式(Okapi BM25)

DL値の意味(Okapi BM25)

DL値はある文書に含まれる総単語数を表す．DL値は文書ごとに存在し，TF値を計算する際の分母と同じ値となる．

DL値の計算式(Okapi BM25)

ある文書d_jにおけるDL値は以下の式から算出できる．

$$dl(d_j)=文書d_jのすべての単語の出現回数の和=\sum_{t_k\in d_j}f(t_k,d_j)$$

また，重要度の算出時には文書集合Dの平均DL値も使用するため，以下の式から事前に算出しておく必要がある．

$$avgdl=文書全体の平均DL値=\frac{\sum_{d_j\in D}dl(d_j)}{|D|}$$

それでは，TF値，IDF値，DL値，文書全体の平均DL値(avgdl)から重要度を算出する式を確認しよう．

Okapi BM25で算出する重要度の意味と計算式

Okapi BM25で算出する重要度の意味

TF-IDF値と同様，Okapi BM25では単語毎の重要度を算出する．また，こちらもTF-IDF値と同様に，Okapi BM25で算出した重要度は文書ごと，単語ごとに存在する．

Okapi BM25の計算式

Okapi BM25の重要度は以下の式から算出する．なお，式中のk₁とbは後ほど解説する．

$$score(t_k,d_j)=idf(t_k)・\frac{tf(t_k,d_j)・(k_1+1)}{tf(t_k,d_j)+k_1・\left(1-b+b・\frac{dl(d_j)}{avgdl}\right)}$$

score(t_k,d_j)の値が大きくなるほど重要度が高いことを，score(t_k,d_j)の値が小さくなるほど重要度が低いことを表す．また，算出式の分子は単語の出現頻度から算出したTF-IDF値に関する計算部分であり，算出式の分母は文書の単語数に関する計算部分であることがわかるだろう．

以上の計算式から，以下のような単語の重要度が高くなる傾向にあることがわかるだろう．
　(1)文書における単語の出現頻度(TF値)が高い
　(2)文書集合での出現頻度(DF値)が低い(IDF値が高い)
　(3)単語数(DL値)が少ない文書に出現している

それでは，式中のパラメータであるk₁とbについて解説する．

Okapi BM25のパラメータ(k₁,b)

◆パラメータk₁
　k₁は主に単語の出現頻度から計算した重要度(TF-IDF値を指す)の影響の大きさを調整するパラメータである．k₁=1.2もしくは2.0とし，k₁=2.0が一番効果的であることが確認されている．

◆パラメータbについて
　bは主に文書の単語数による影響の大きさを調整するパラメータである．0.0から1.0の間で設定し，b=0.75が一番効果的であることが確認されている．なお，b=0.0とした場合，文書の単語数による影響をなくした結果を得ることができる．

TF-IDFおよびOkapi BM25の応用可能性

TF-IDFやOkapi BM25で算出した単語の重要度は主に情報検索やトピック分析の分野で利用され，文書の特徴によるカテゴライズ等に応用されている．また，検索ワードに近いカテゴリの文書をユーザに提示することで，Google検索に近い機能を実装できるようになるだろう．その他にも，文書の要約(長文を短文にまとめる)や見出しの推定にも単語の重要度を利用することができるため，TF-IDFやOkapi BM25は幅広い分野で注目されている．

参考

・tf-idf – wikipedia
・TF-IDFで文書内の単語の重み付け
・tf-idfについてざっくりまとめ_理論編
・【対数】対数はなんの役に立つのか
・確率的情報検索 Okapi BM25 についてまとめた
・Simple, proven approaches to text retrieval
・Okapi BM25 – Wikipedia

人工知能・機械学習・自然言語処理周辺の技術情報

目次