今回は潜在意味解析(Latent Semantic Analysis: LSA)と特異値分解(Singular Value Decomposition: SVD)について解説します.
LSAは文書の分類や,情報検索の分野(この分野ではLSIとして知られる)などに使われるトピックモデルの代表例として知られています.
このモデルを使うと,単語と文書のそれぞれの組み合わせについて,類似度を測れるようになります.
目次
潜在意味解析(LSA, LSI)とは
特異値分解(SVD)
LSAのアルゴリズム
LSAの応用
LSAの問題点
参考文献
潜在意味解析(LSA, LSI)とは
潜在意味解析(Latent Semantic Analysis: LSA)とは,1990年にDeerwesterらが発表した,文章の自動インデックス化,検索の方法である.検索の分野では潜在意味インデックス(Latent Semantic Indexing: LSI)とも呼ばれる.高次元の文書群から,与えられたクエリに意味的に関連する文書を見つけてくるために作られた.単語-単語,単語-文書,文書-文書の類似度を求めることができる.
この手法では高次元の文書の行列を,特異値分解(SVD)という線形代数的手段で低次元に縮約し用いている.圧縮されてできたベクトル空間内では,近い概念は近くに,遠い概念は遠くにプロットされる.低次元に縮約することによって,疎らなデータやノイズが多いデータに対応できる.また,メモリに乗らない巨大なデータにも対応できる.
時代的背景
LSA以前の時代に作られた情報検索の手法では,語の意味そのものに着目していた.しかし,語の意味は多義語として知られるように,文脈によって変わることもあり信用性に欠ける.また,単語Aで検索した時にその類義語の単語Bの結果もある程度考慮しなくてはならないが,これに対応するのに困難していた.そのため,より信頼性の高いエンティティの集合に置き換える必要があるとLSAの提案者たちは考えていた.
特異値分解(SVD)
LSAのアルゴリズムのうち大切な部分がこの特異値分解(SVD)である.まずは,この技術について解説していく.
特異値分解(SVD)とは
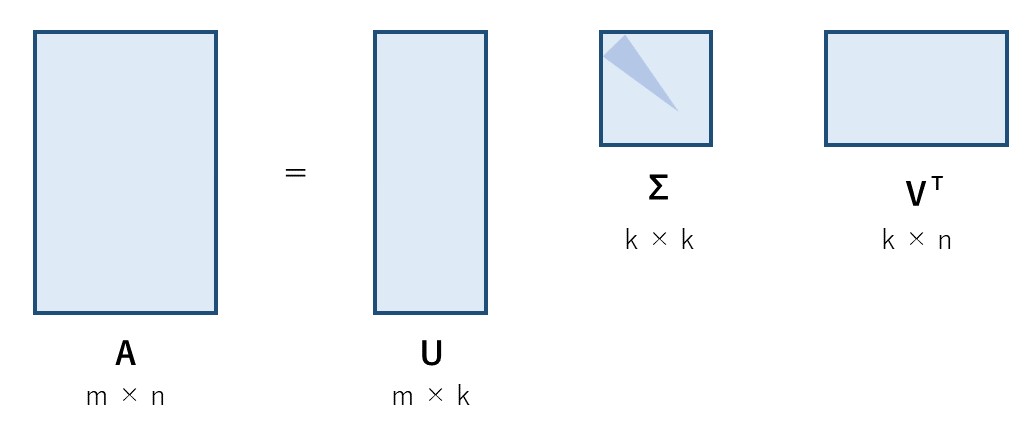
特異値分解(Singular Value Decompositon: SVD)とは一言でいうと上の図のように,任意の実行列が二つの直交行列と特異値からなる対角行列の内積に分解できるということである.
右辺の,左右の行列($U$と$V^T$)の各列をそれぞれ,右特異ベクトル,左特異ベクトルと呼ぶ.また,それぞれ入力の行,列ベクトルの張る空間の正規直交基底を表す.ここで,行列$A$の特異値とは,$A$とその随伴行列$A^{*}$(複素共役かつ転置行列)であるとの積のそれぞれの固有値における,非負の平方根のことである.つまり,真ん中の行列$Σ$の対角成分の二乗は固有値である.特異値は各基底の重要度を表している.
(LSAの論文中では,$X = T_{0}S_{0}D_{0}^{*}$と記されている.T:term, S:semantic space, D:documentを表していると思われる.)
SVDの証明概略
以下の式が成り立つことを示す.
$$A = UΣV^T$$
任意の$m×n(m\geq n)$実行列$A (rank=k)$において,$A^{T}A$は対称行列である.
(∵ $(A^{T}A)^{T}=A^{T}A$)
そのため,正規直交基底を用いて対角化可能である.
また,固有値は実数で,固有ベクトルは互いに直交する.
$A^{T}A$を固有値の定義に従い固有分解する.
$A^{T}AV=ΛV$
ただし,$Λ$は$n$個の固有値
$λ_1>…>λ_r>0, λ_{r+1}=…=λ_k=0$
からなる対角行列$Diag(λ_1,…,λ_k)$である.
また,$V$はこれに対する固有ベクトル(正規直交基底)を列にもつ行列である.
$V=[v_1 v_2 … v_k]$
$i\leq r$の時,固有値の定義式から以下が成り立つ.
$A^TAv_i = λ_iv_i$
$i\geq r+1$の時には,以下が成り立つ.
$A^TAv_i = 0v_i = 0$
ここで,$i\leq r$の時$u_i=\frac{Av_i}{\sqrt{λ_i}}$とおく.
$u_i^Tu_j$
$= \frac{1}{\sqrt{λ_i}\sqrt{λ_j}}(Av_i)^T(Av_j)$
$= \frac{1}{\sqrt{λ_i}\sqrt{λ_j}}v_i^TA^TAv_j$
$= \frac{1}{\sqrt{λ_i}\sqrt{λ_j}}v_i^Tλ_iv_j$
$= \frac{\sqrt{λ_j}}{\sqrt{λ_i}}v_i^Tv_j$
$= δ_{i,j}$
となるため,$u$もまた正規直交系をなす.
これを並べて以下のように置く.
$U=[u_i … u_m]$
$u$が正規直交系をなすことから,$U$は直行行列である.
($UU^{T}=U^{T}U=E$)
$U^TAV$
$= U^T[Av_1, … , Av_n]$
$= U^T[\sqrt{λ_1}u_1, … , \sqrt{λ_r}u_r, 0, …, 0]$
$= [\sqrt{λ_1}U^Tu_1, … , \sqrt{λ_r}U^Tu_r, 0, …, 0]$
$= Diag(\sqrt{λ_1},…, \sqrt{λ_n})$
となる.
これを$Σ$とおくと以下のようになる.
$U^TAV=Σ$
これに左から$U$を,右から$V^T$をかけることで以下を得る.
$UU^TAVV^T = UΣV^T$
$A = UΣV^T$
(証明終了)
LSAのアルゴリズム
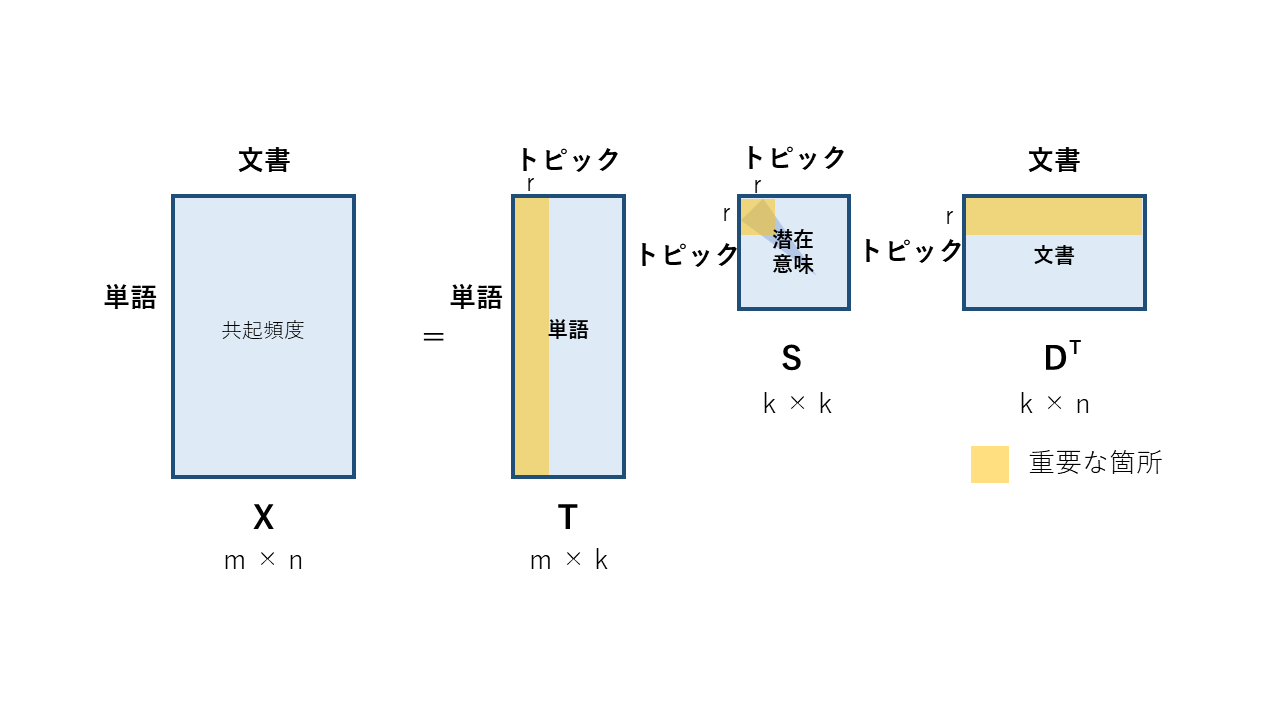
SVDがわかれば,LSAのアルゴリズムの大方がわかったと言っても過言ではない.LSAではSVDで求まった特異値を影響度の少ない順に削っていくことによって次元を削減する.その後,次元削減された特異値の行列を用いて類似度を算出する.これを上図により図解した.オレンジ色の部分は次元削減後の重要部分を表している.
以降,Deerwesterらの論文(原著)に合わせるため,SVDで単語とドキュメントの行列Xを分解した結果を,以下の表記を用いて表す.
$$X = TSD^T$$
この行列の値には共起回数(各文書における単語の出現回数)が入り,TF-IDFで重みづけされることが一般的である.
次元の圧縮
SVDによって得られた分解のうち,真ん中の特異値行列をその要素である特異値の小さい順に0にしていく(上図参照).0にする特異値の個数はパラメータとして設定され,0にした個数が少ないほど元の行列に近く,多いほど圧縮度の高い行列となる.パラメータが最適な値の時この行列は,元のデータを表すのには十分でありつつ,あまり重要ではないデータやノイズを復元するのには不十分であることが期待できる.
計算の際には,0にした箇所に対応する部分は削って計算する.こうすることにより,計算量を削減できる.
また,こうして得られた行列は各次元において,元の行列の最小二乗(フロベニウスノルムが最小)の近似となることがわかっている.
各類似度は,それに対応するベクトルのドット積で表す.これは,自然言語処理の分野でよく使われているコサイン類似度の分子の部分にあたる.
単語-単語の関連性を求める
それぞれの行列は次元削減をした後の行列とする.
$T$が直行行列,$S$が対角行列であることに注意し,$X$のそれぞれの行に対してドット積を求めればよい.
$$XX^T = TS^2T^T$$
文書-文書の関連性を求める
$D$が直行行列,$S$が対角行列であることに注意し,$X$のそれぞれの列に対してドット積を求めればよい.
$$X^TX = DS^2D^T$$
単語-文書の関連性を求める
$X$自体がこれらの関連性を表している.
$$X = TSD^T$$
LSAの応用
検索エンジンやレコメンドエンジンなどの情報検索の分野や,概念の学習過程の計算モデルとして心理学の分野でも用いられる.
また,文章のみでなく,元の行列をユーザーとその性質などに置き換えることも可能である.例えばECサイトにおけるユーザーの購買データを集めたものを行列とすることで,購買履歴から似ているユーザーが買っている商品をレコメンドすることができる.
LSAの問題点
・各トピックは互いに直交しており,それらの関連性はみることができない.
・出現頻度しか見ていないため,逆説の接続詞などの文脈構造が考慮されていない.
・トピックに名前がついていなく,それぞれが何を表すトピックなのかわからない.
参考文献
【論文】
S. Deerwester, S.T. Dumais, G.W. Furnas, T.K. Landauer, and R. Harshman. Indexing by Latent Semantic Analysis, Journal of the American Society for Information Science, 41(6):391-407, 1990.
【Webサイト】
ECEN 601: Linear Network Analysis

