人工知能・機械学習・自然言語処理周辺の技術情報

ミエルカAI TOP > メディア > 非エンジニア向け > 【人工知能(AI)】ディープラーニングの仕組み！中学生でもなんとなくわかる！【入門】
2018-06-25

【人工知能(AI)】ディープラーニングの仕組み！中学生でもなんとなくわかる！【入門】

人工知能（AI）やDeepLearning（ディープラーニング），この頃よく聞きますよね．
しかし，いまいち何なのかよくわからないという人は多いのではないでしょうか．
私の周りの人たちも教養として興味はあるけれども，数式が出てくると何がなんだかという人が多いようです．
また，人工知能やディープラーニングをビジネスに応用したいけど何ができるのか全く見当もつかないといった人も多いようです．
そもそも，ディープラーニングとはなんのことなんでしょう．AIや機械学習との違いはどこにあるのでしょう．
そこで今回はエンジニアや理系の学生でない人に向けて，ディープラーニング（主にその基礎となるニューラルネット）の仕組み，原理，アルゴリズムや種類，それが何の役に立つのかについて解説してみようと思います．
このような場合には，よくわからない記号が出てくる数式は避けるべきだと思います．
しかし，すべてを包み隠されて説明しても納得できないと思うので，今回は入門者や初学者を対象に中学校で習う範囲の知識で，簡単になんとなく理解できるように工夫して書いてみます．
難しい部分は数式の代わりに図解していきます．
もしこの記事で興味を持ってもっと知りたいと思ったら，線形代数，微分積分，統計学を勉強してみることをおススメします．

目次

機械学習とは
ニューラルネットワークとは
最急降下法
バックプロパゲーション
ニューラルネットの応用
DeepLearning(ディープラーニング)とは
まとめ

機械学習とは


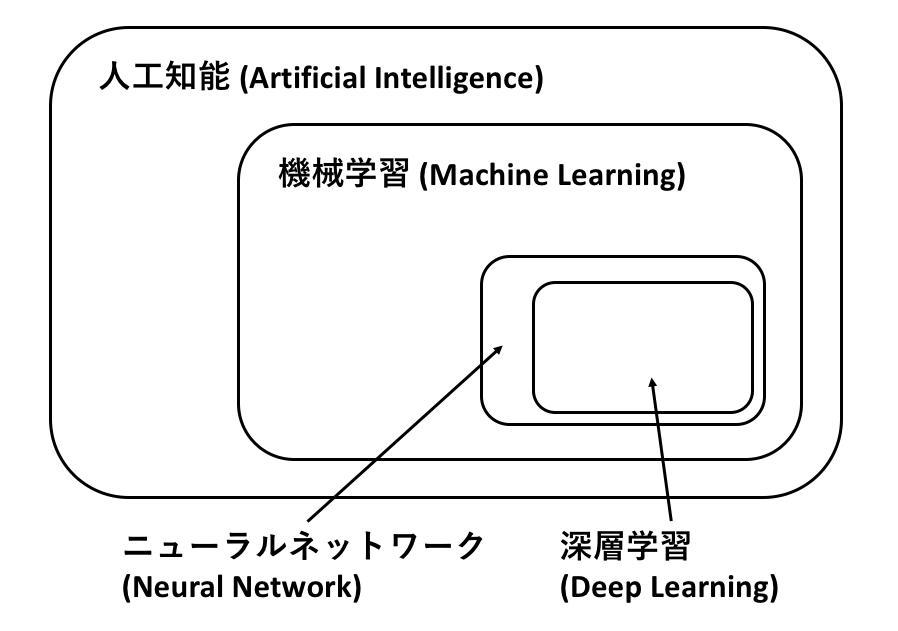
DeepLearning（ディープラーニング：深層学習）は，Machine Learning（マシンラーニング：機械学習）の一部でである．
Machine Learning（マシンラーニング：機械学習）は，Artificial Intelligence(AI：人工知能)の一部である．
つまり，ディープラーニングはAIであり，かつ機械学習でもある．また，機械学習もAIである．
ここでいう人工知能(AI)とはアニメや映画に出てくる万能ロボットのようなものではなく（これは汎用人工知能と呼ばれる），主にコンピューターに認識，判別，回帰により，特定の一つの問題を解かせるための手段といった認識が正しい．
残念ながら，今日のAIは世間が考えるほど何でもできるわけではいのである．その手段がたくさん提案され報道されているため，囲碁や将棋もできれば自動運転もできるロボットがいるような錯覚に陥るのだと思う．

機械学習とは

wikipediaによると，機械学習は以下のように説明されている．
”機械学習（きかいがくしゅう、英: machine learning）とは、人工知能における研究課題の一つで、人間が自然に行っている学習能力と同様の機能をコンピュータで実現しようとする技術・手法のことである。” – 機械学習(wikipedia)
つまり，機械に勝手に学習してもらおうということである．
条件分岐などのルールを使って，こうなったらこうして，こっちだったらこうしてという方法は機械学習ではない．
こうだったら，こっちだったら，といったルールそのものを抽象的に獲得しようとするのが機械学習である．
ルールベースでつくられたプログラムでは，そのルールでカバーしきれていない範囲の事象に対応できない．
しかしながら機械学習では，統計的手法を用いて手元のデータからルールを抽象的な形で獲得しようとするため未知のデータに対する推定についてもある程度の汎化性がある．

機械学習でできること

クラス分類（識別）
クラス分類とは，そのデータがどのカテゴリーに属するかを判別することである．
例えば，ある人の身長と体重のデータから，その人は男性か女性かを判定するといった手法がこれに当たる．
この場合以下のような，「この身長，この体重（データ）は男性（正解ラベル）です」といった教師データと呼ばれるデータをもとに学習し判別を行う．

  • 身長：178cm，体重：78kg -> 男性
  • 身長：168cm，体重：58kg -> 男性
  • 身長：149cm，体重：47kg -> 女性
  • 身長：162cm，体重：56kg -> 女性

このようにデータとラベルのセットをもとに行う学習を，教師あり学習という．
一方，ラベルがない学習は教師なし学習という．
教師なし学習ではそのデータの性質から分類などを行う．
例えば，上で例として挙げたデータを用いて男女を分類するのであれば，縦軸を身長，横軸を体重としたグラフ（各軸は逆でも良い）で，男女のデータをうまく分けるような線を引いてやればよい．
機械学習では，データからこの線を自動で導くことができる．

回帰
回帰とは，与えられたデータがどんな関数(入力する数と出力する数の関係のこと．y=3xなど．)で求められるかを推定することである．
例えば，男性の身長と体重のデータをたくさん集めてそれを学習し，ある男性の体重から身長を推定するといったことに用いられる．
この場合も，この身長ならこの体重になるといった教師データを用いた教師あり学習を行う．

クラスタリング
クラスタリングとは，いくつかのデータからその類似度を用いてグループを作ることである．
データ自身の類似度や距離といった性質を用いて分類をするため，これは教師なし学習に分類される．

ニューラルネットワークとは

ディープラーニングを知るうえで，ニューラルネットワークへの理解は不可欠である．
ニューラルネットワークは機械学習の一分野で，その中にディープラーニングがある．

（人間の）ニューラルネットワーク

ニューラルネットワーク（通称：ニューラルネット）とは，人間の脳の構造を模してつくられた数学モデルである．
このモデルは人間の脳のものと区別するために，しばしば「人工ニューラルネットワーク」とも呼ばれる．
モデルの理解には，そのもととなった人間の脳について知る必要がある．
まずは，そちらについて説明する．
とはいえ，こちらの説明はすこし難しいため，人工ニューラルネットワークまで飛ばしても構わない．

人間の脳には神経回路網（ニューラルネットワーク）と呼ばれる，神経細胞（ニューロン）からなるネットワークが存在する．
ここでは，単一の神経細胞がほかの神経細胞と結びつくことにより，複雑なネットワークを形成している．

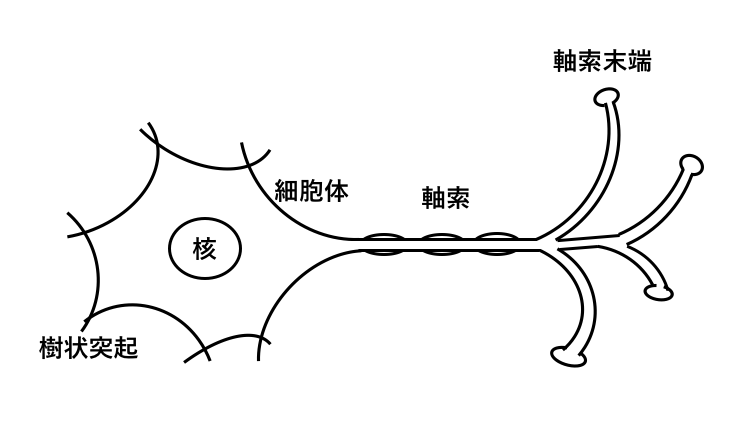
神経細胞には，樹状突起，細胞体，軸索，軸索末端と呼ばれる部位が存在する．
これらの役割についてみていこう．

樹状突起(Dendrite)
ほかの細胞からの電気的信号を受け取る．
入力装置のようなもの．

細胞体(Soma)
細胞として機能する．

軸索(Axon)
電気的信号を伝える，出力装置のようなもの．
末端は軸索末端(Axon terminals)と呼ばれ枝分かれしている．
この末端部分が他の神経細胞の樹状突起に接続する．
この接合部分をシナプスと呼ぶ．
直接くっつくわけではなく，シナプス間隙と呼ばれる隙間が空いている．
ここの隙間では，ナトリウムイオンのやり取りにより信号が伝えられる．

情報の伝達
細胞内の電位はその外と比べて常に相対的に負（静止電位）であるが，他の神経細胞から刺激を受けることによりその電位が一瞬だけ正（活動電位）になった後，再び元の電位に戻ることがある．これを発火(スパイク，インパルスとも)という．
この発火は外部からの刺激の強さがある値以上になったときに起こる．この値を閾値と呼ぶ．閾値に達さない刺激ではすぐに静止電位に戻る．
またニューロンは発火した際に，軸索を通して軸索末端にあるシナプスから神経伝達物質を放出し他のニューロンの電位を変化させる．
ニューロンがほかのニューロンを発火させたときには，その間の結合が強まる．また，長期間発火しなかったニューロンとの結合は弱まる．これをヘブ則という．
つまり，繰り返し発火するようなニューロン間の結合は強化されていく．
こうして記憶が形成され学習していると考えられている．

（人工）ニューラルネットワーク

上で説明した人間のニューラルネットを模した数理モデルである「（人工）ニューラルネットワーク」について説明していく．
まずは，このニューラルネットを形成する素子である「人工ニューロン」についてみていく．

人工ニューロン

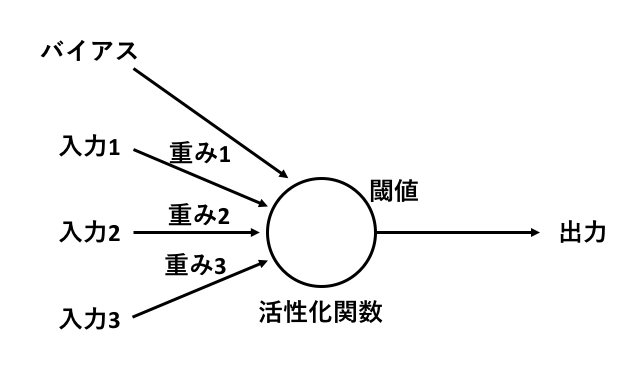
人工ニューロンは，人間の脳のニューロンを模した数理モデルである．
人間の脳のニューロンと同様に他のニューロンからの入力を受け取り，それを処理して（実際には結合強度を掛けて足し合わせる），閾値（これを超えたら出力するという値）を超えたら出力をする．
初期のモデルであるマカロック・ピッツモデルは上記の通りで，0か1の入力を受け取りそれの重み付きの和がある閾値を超えたら1，そうでなければ0を返す．
この時，閾値を超えたら1，超えなかったら0を返すといったステップ関数を，ニューロンの出力を制御するための活性化関数として用いる．
この重みと閾値を変えることにより，学習（教師データとして与えた入力と出力の関係に近づくようにこれらを調整すること）を行う．
しかし，このモデルは連続的（グラフにしたとき線が途切れないこと）でなく，微分(ある地点において関数の傾きを求める操作)ができない（要するに不都合な）ため現在はシグモイド関数を用いた，次のようなモデルが用いられている．
その前に，シグモイド関数とは，以下のような形をした関数である．

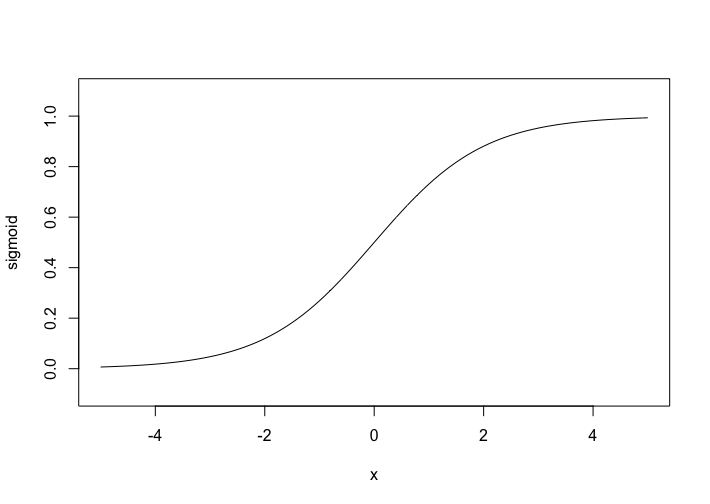
シグモイド関数は，どこでも微分することができ（関数の傾きを求められる），連続（関数のグラフが途中で途切れていない）である．
入力する値は一般的には実数値をとる．実数値とは，-20, 3.14, 234, 2/29などの普段我々がいる世界で使われる数値である．ニューラルネットでは実用的にはその入力を，-1から1くらいに標準化(比を保ったまま縮めること，たとえば，$[-10, -5, 0, 5, 10]$というデータをこの範囲に収まるように標準化すると，$[-1, -0.5, 0, 0.5 , 1.0]$となる)されることが多い．
また出力する値も実数値である．

人工ニューラルネットワーク
ここで例として，これを4つ組み合わせたニューラルネットを考える．
さらに，これを2つずつの層にして，それぞれを入力層と出力層とする．

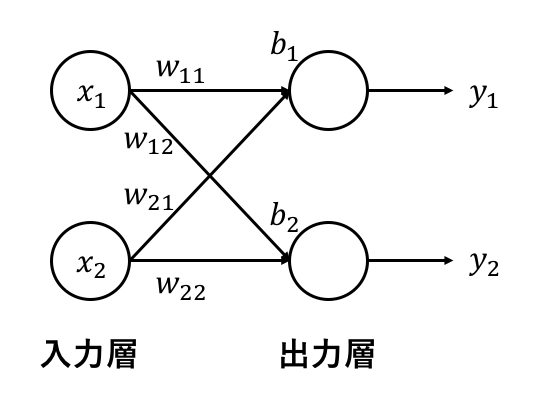
ここで，入力する値をx1，x2，結合強度（重み）をw11，w12，w21，w22，バイアス（閾値のようなもの）をb1，b2，出力をy1，w2とおく．
また，シグモイド関数をsigmoid(x)とおく．これは，xをシグモイド関数に与えるとその出力はsigmoid(x)になることを意味する．
すると，出力を求める式は以下のようになる．

$$y_{1} = sigmoid\left(w_{11}x_{1} + w_{21}x_{2} + b_{1}\right)$$
$$y_{2} = sigmoid\left(w_{12}x_{1} + w_{22}x_{2} + b_{2}\right)$$

つまり，出力の値はそれぞれ，つながっているそれぞれ入力と結合強度（重み）の積をすべて足し合わせ，それにバイアスを足したものを，シグモイド関数（活性化関数）に入れたものである．

層の数やニューロンの個数が増えても行う計算は同じである．
接続しているニューロンからの出力を重みを付けて受け取りそれらを足し合わせ，活性化関数（シグモイド関数）に入れた値を出力とする．
3層以上の場合は，最初の層を入力層，最後の層を出力層，それ以外を中間層と呼ぶことが一般的である．
学習は，これらの重みを最適化することにより行われる．
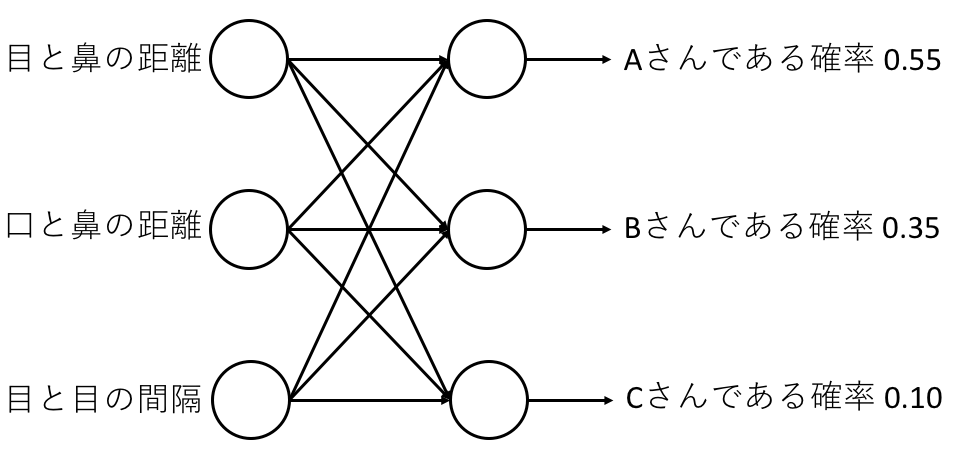
また，クラス分類に用いる際には，出力層の活性化関数をソフトマックス関数というものにする．
出力層のニューロン数は，分類したいクラスの分用意する．
このソフトマックス関数は，出力層のニューロンの出力する値の和が1になるように調整してくれる．
こうすることで，出力は入力が各クラスに分類される確率となる．

最急降下法

ニューラルネットの学習方法を勉強する前に，最適化の分野で一般的に用いられる最急降下法（Gradient descent）について知る必要がある．
これは，関数の最小値を探索的に求めためのアルゴリズムである．
ここでいう関数とは多変数のもの(関数の入力にあたる数が複数あるもの)を指すことが多いが，ここでは簡単のために単一の変数からなる関数を考える．
多変数の場合も各変数について以下の操作を行うだけなので問題ない．
二次関数なら平方完成すればよいが，実際に人工知能で用いる関数は変数がいくつもあり高次元のものなので，解析的には解くことは不可能である場合が多い．

最急降下法

最急降下法は，一言でいうと関数が最小値を取るときのパラメータ（関数を定義するのに必要な変数）の値を求める方法である．
ディープラーニングでは，教師データと出力との誤差を表す関数を，最小化するような重み（パラメータ）の値を求めるためにこの方法を応用したアルゴリズムが用いられる．

ここで，例として

$$y = 2x^{2}-4x-1$$

という関数を考える．
x=1の時に最小値y=-3をとるが，これを解かずに求めることを考える．
最急降下法では，グラフ的特徴から最小値を求めるという方針で考えていく．
x=2の時，y=-1だが，このときの関数の傾きについて考えると，この関数は左下がりになっている．
x=0の時，y=-1だが，この時には傾きは右下がりなことがわかる．
この傾きが右肩上がりなのか，右肩下がりなのかを求めるのが微分という操作である．

微分は高校数学の分野であるが，yがxやx2からなる関数の微分は簡単なのでやってみる．
この関数に限って言えば，微分はxの肩に乗っている数を，その係数にかけてやって，肩の数を-1すればよい．
つまり，この関数の微分値は，4x-4となる．
これにx=2を代入すると，4となる．
また，x=0を代入すると，-4となる．
この4や-4を微分係数といい，その値の正負でその時点での傾きを判定する．
微分係数が正なら増加中（右肩上がり），負なら減少中（右肩下がり）を表している．
最急降下法の基本的な考え方は，関数の最小値を求めるのなら，微分係数と反対の方向に少しずつ動かしてやればよいというものである．
イメージとしては，近く谷にボールを転がすイメージである．

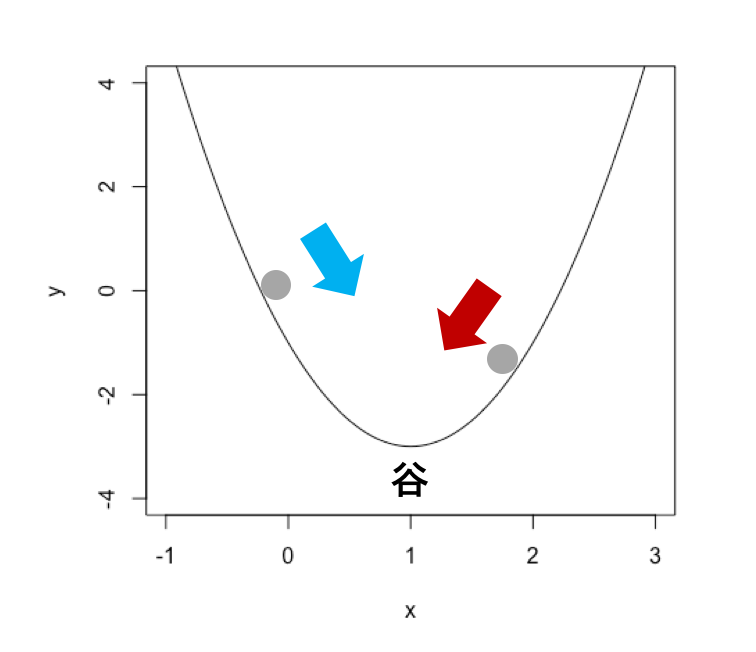
最急降下法の実際の式は以下のようになる．

$$x^{k+1} = x^k – \alpha\mathrm{grad}f\left(x^{k}\right)$$

$\mathrm{grad}f\left(x^k\right)$は勾配とよばれるが，$x^k$における微分係数（傾き）を表すものと考えてよい．
肩に乗っているkはk回目のパラメータを意味している．つまり，左辺がk+1回目のxで，右辺がk回目のxとなり，その関係を表す式になっている．
αは0.05くらいの値に設定される，学習のパラメータ（状況に応じて好きに設定して良い）である．
これを大きくすると学習が早く進むが，極小値付近での精度が落ちる．
小さいと学習が遅くなる．
つまり，この式では，現在のxから，ほんの少し($\alpha\mathrm{grad}f\left(x^k\right)$)だけ谷の方に動かしたものを次(k+1回目)のxにするということを表している．
これを繰り返し用いることによって，近くの最小値が求まる．

しかしながら，谷がいくつもある関数だと落ちた谷が全体の最小値であるかどうかわからない．
このように，局所的な最小値のことを局所最適解，全体的な最小値のことを大域最適解と呼ぶ．
実際のディープラーニングでは局所最適解から抜け出すために，最急降下法ではなく，これに工夫をしたアルゴリズム(NAG，Ada Grad, Adamなど)によって学習を行う．
やっていることのイメージとしては，ボールを谷に落とす際に重力やブレーキを働かせたりなどの工夫をしている．

バックプロパゲーション

バックプロパゲーション（誤差逆伝播法）はニューラルネットの学習方法である．
ディープラーニングもニューラルネットワークの一分野であるため，学習にはこのバックプロパゲーションも用いられる．
ニューラルネットはその重みを調整することにより，与えた値に対してほしいの出力を得られるように学習する．
この時の重みの調整方法がこのバックプロパゲーションである．

誤差関数

ある値を与えた時のニューラルネットの出力と，その時に欲しい出力（教師信号）との誤差を求める関数を誤差関数（損失関数，コスト関数などとも呼ばれる）と呼ぶ．
誤差関数にはいろいろな種類があるが，ここでは一番簡単な二乗誤差からなる誤差関数について考える．
二乗誤差は，出力ykに対する，教師信号がtkであるときに，$\frac{1}{2}\left(y_k – t_k\right)^{2}$（つまり，カッコ内を二つ掛け合わせたもの）で定義される．
二乗（二回掛け合わせ）するのは，常に誤差を正の数として考えるためである．
二乗しなければ$y>t$のときは正だが，$y<t$の時には負になってしまう．
また，1/2した理由は，微分したときに肩の2が前に出てくることから，あらかじめ簡単化しておこうという魂胆である．
パラメータの最小化問題において，関数に1/2のような正の係数をかけることは，パラメータの最適化に特に影響を及ぼさない．
ニューラルネットの出力は，結局は重みの値と，ニューロンの配置によって決まるため，その学習では，この誤差関数ができるだけ小さくなるように重みを決める．

誤差逆伝播（バックプロパゲーション）

誤差関数の値をニューラルネットの重みの更新に使うことを考える．
先ほど説明した最急降下法などの最適化法を用いて，誤差関数を最小化していく．
この場合，最急降下法の項で関数としていたものが誤差関数にあたり，変数としていたものが重みになる．
つまり，重みについての最適化を行うことにより誤差関数を最小化する．
誤差の情報は，出力に対してしか与えられないため，これをどうにかして重みに与えてやりたい．
これを解決するのが誤差逆伝播（バックプロパゲーション）である．
この方法では，出力側から入力側にかけて誤差の情報を伝播させて（伝えて）いく．
各出力には，それを出力したニューロンにつながるニューロンからの重みが関与している．

誤差関数E(x)を展開してみると，

$$
\displaystyle
E\left(x\right) =
\frac{1}{2}\left(y_{k} – t_{k}\right)^{2} =
\frac{1}{2}\left(sigmoid\left(\sum_{j} w_{jk}x_j + b_k\right) – t_{k}\right)^{2}
$$

となる．これをwjkに対して微分すると，wjkに対する傾きが求まる．
あとは，これを最急降下法のような最適化法で最適化（重みを調整して誤差が少なくように）すればよい．

層が何層になっても，各重みに対するその微分はその次の層（より出力側の層）の微分を使って求めることができる．（ここが肝心）
（これを微分の連鎖律（チェーンルール）などと呼ぶ．）

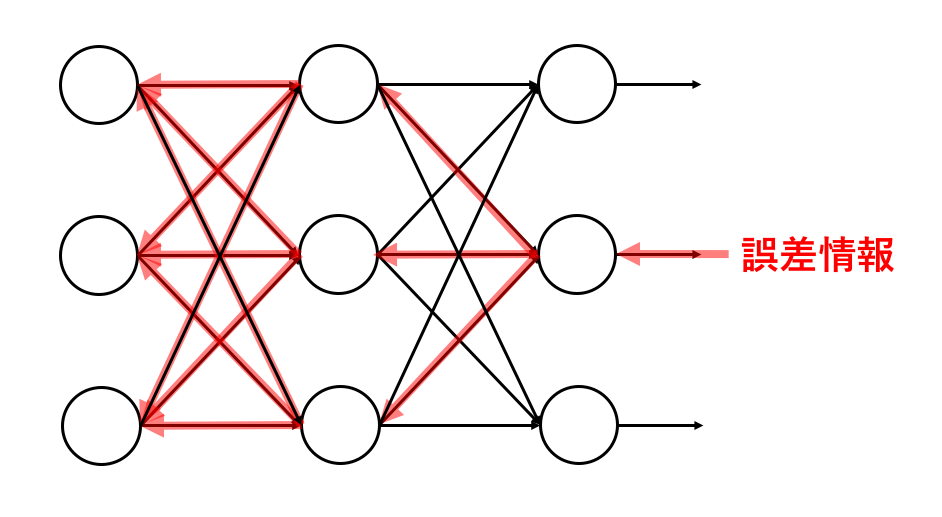
こうすることにより重みを調整し学習することができる．

ニューラルネットの応用

さて，ニューラルネットの学習まで理解できたが，いったい何の役に立つのだろうか．
ニューラルネットでできることはざっくりと，分類，回帰に分けられる．
それぞれがどのような場面で役立つのかについて紹介する．

クラス分類の応用例

有名な例として，認識がある．
顔画像の認識や，手書きの数字の識別などがよく行われている．
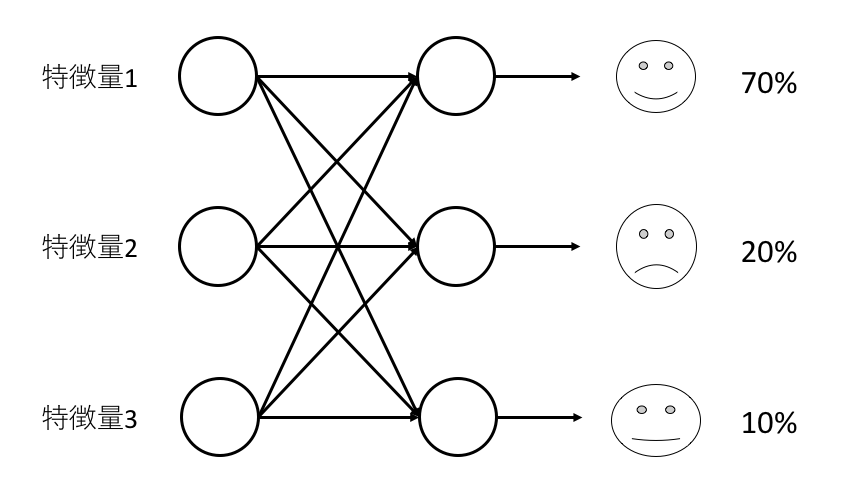
例えば顔画像からその人がAさん，Bさん，Cさんの誰なのかを識別（認識）するといったタスクを考えてみる．
通常のニューラルネットでは数値しか用いることができないため，顔画像の特徴量というものを定義する必要がある．
特徴量とは，機械学習の分野で用いられる言葉で，データの特徴を定量的に表したものである．
モデルの予測精度は，この特徴量をいかにうまく設計できるかに大きく依存する．
顔画像の場合にはその特徴量に，目頭，目じり，眉，鼻翼，輪郭などから取得した座標間の距離などを用いる．
これをニューラルネットの入力に入れ，誰の顔なのかを判定し出力するように学習させる．

回帰の応用例

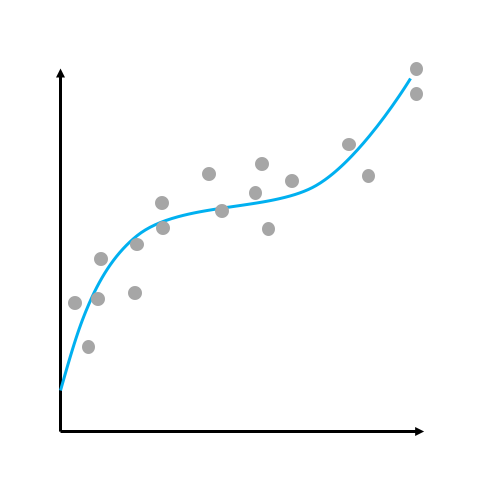
回帰はなんらかの値の組から決まるなんらかの値を予測することに幅広く用いることができる．
例えば，土地の広さや，地価，部屋の広さ，部屋数などの特徴量から住宅の価値を推定することなどができる．
入力にはこれらの特徴量を入れ，出力には住宅の価値を推定するように学習させる．

このように，データがあればそのデータをもとに分類問題を解いたり，未知のデータを推定することができる．
そのためデータを持つ企業では機械学習をビジネスに応用する機会がある．
また，ニューラルネットの学習にはそのデータを特徴づけるための特徴量が必要なことが分かった．
機械学習の分野では，このように特徴量の設計がとても重要になってくる．特徴量がわかりやすく確実なものなら機械学習を用いればよい．
しかし，例えば一般画像認識（ある物の画像から何かを識別するタスク）などでは人手で特徴量を設計するのはとても難しい
そのためこの分野では長い間，顕著な精度の向上が見られなかった．
このような状況で第二次人工知能ブームと呼ばれるブームは下火になりつつあったが，2012年にディープラーニングが革命を起こした．
ディープラーニングを用いたモデルが一般画像認識のタスクにおいて，今までのどのモデルよりもはるかに上回る精度を出したのである．

DeepLearning(ディープラーニング)とは

ディープラーニングはいわばニューラルネットワークの進化系である．
ディープラーニング以前の機械学習やニューラルネットの分野では，人手による特徴量の設計が必要だった．
しかし，ディープラーニングは大量のデータからその特徴量を自動で抽出し学習するといった機構を持つ．
これこそがディープラーニングのすごいところである．

ニューラルネットのとの違い

ディープラーニングはニューラルネットの一分野であり，おそらくその厳密な定義はない．
一般的にはニューラルネットの層を4層以上に深くしたものを深層学習（ディープラーニング，DeepLearning）と呼ぶ風潮らしい．
また，特徴量を自動で獲得させよう，つまり文章や画像や音声などのデータをそのまま与えて回帰や分類を行おうとさせるのがディープラーニングの特徴である．

ディープラーニングのモデルの種類

ディープラーニングのモデルにはたくさんの種類があるが，大きく分けると画像系に用いられるCNN系統のモデルと，時系列データに用いられるRNN系統のモデルに分かれる．
どちらとも学習の流れや使い方は基本的なニューラルネットワークと大差はないが，それぞれ特殊な機構を持っている．

CNN(Convolutional Neural Network: 畳み込みニューラルネットワーク)
CNNは生物の視覚野に着想を得た機構を持つ，ニューラルネットワークである．
主に画像を入力にする際に用いられ，2012年に第3次人工知能ブームのきっかけとなった，ILSVRCという一般画像認識の大会でトロント大学のジェフリー・ヒントンらが用いたモデルもこれである．
CNNにはパターンの特徴を抽出する畳み込み層と，情報を圧縮することにより位置のずれなどを吸収するプーリング層があり，これらを交互につなげたのち，全結合層と呼ばれる2層のニューラルネットワークに接続される．
もちろんこのネットワークもバックプロパゲーションで学習させることが可能で，誤差関数の微分を連鎖律を使って伝播させていく．

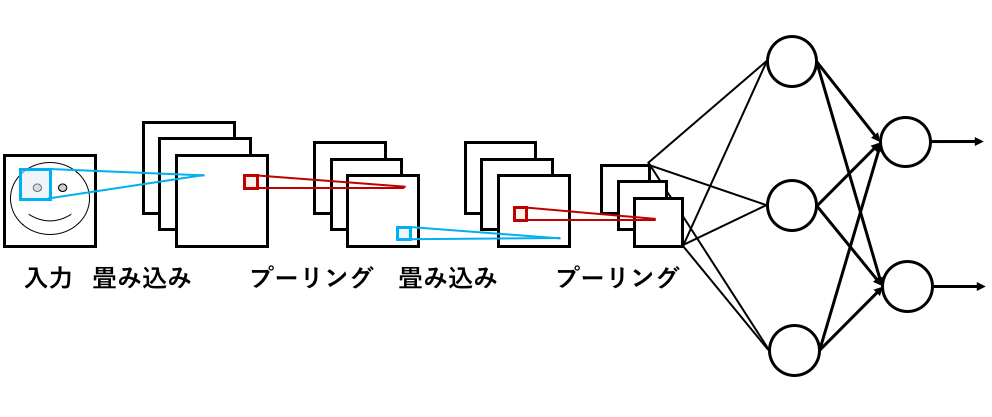
cnn_image

畳み込みニューラルネットワーク

ちなみにこのようなモデルを初めて作ったのは日本人の福島邦彦氏である．

RNN(Recurrent Neural Network: リカレントニューラルネットワーク)
RNNは時系列データの学習に用いられるモデルである．
時系列データとは，入力が時事刻々と変化するようなデータのことで，文章や音声や株価なのがこれにあたる．
たとえば文章を学習する際には，1時刻ごとに単語を表す情報をこのRNNに入れていく．
そして，1時刻ごとに何らかの値を出力していく．

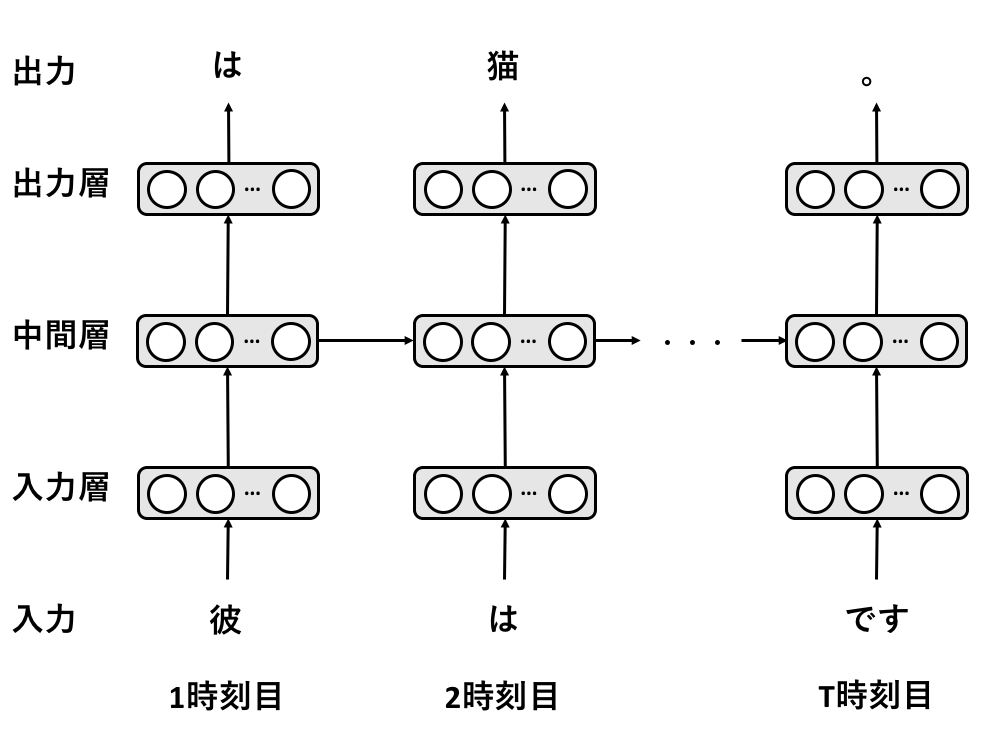
RNN_image

RNN

RNNは最初に説明した基本的なニューラルネットワークと同様に，入力層，中間層，出力層を持つ．
また中間層の出力を，次の時刻の中間層の入力に用いるといった再帰的機構を持つ．
この機構のおかげでデータの時間的な変化を学習することができる．
現在の自然言語処理と呼ばれる分野の研究では，これを発展させたLSTMと呼ばれるモデルを用いたものが盛んである．
LSTMはRNNにゲートと呼ばれる機構を加え，より効率的に学習できるようにしたであるである．
主に，機械翻訳や文章の生成などのタスクで用いられる．

まとめ

ニューラルネットワークは，その重みを調整することにより，データの入力と出力間の関係性を学習するモデルである．
DeepLearning（ディープラーニング，深層学習）とは，深層のニューラルネットワークを用いた機械学習のことで，大量のデータをもとにその特徴を学習することができる．
その学習は誤差の情報を連鎖的に逆伝播し重みを調整することにより行われている．
大量のデータを持つ企業では機械学習やディープラーニングをビジネスに応用する機会がある．

関連記事はこちら

Copyright (c) Faber Company, Inc. All Rights Reserved. プライバシーポリシー