【技術解説】HMMに基づいたViterbiアルゴリズムによる解推定手法(例題つき)

執筆：金子冴

今回は，形態素解析器であるMeCab，Chasen，JUMANで解探索アルゴリズムに採用されているViterbiアルゴリズム(Viterbi algorithm)について解説する．

Viterbiアルゴリズム(Viterbi algorithm)とは

アルゴリズムの解説にうつる前に，まずは概要を理解しよう．

Viterbiアルゴリズムの概要

“ビタビアルゴリズム（英: Viterbi algorithm）は、観測された事象系列を結果として生じる隠された状態の最も尤もらしい並び（ビタビ経路と呼ぶ）を探す動的計画法アルゴリズムの一種であり、特に隠れマルコフモデルに基づいている。” – ビタビアルゴリズム(wikipedia)

上記の概要を見るに，Viterbiアルゴリズムを理解するためには事前に動的計画法と隠れマルコフモデル(HMM)について理解する必要がありそうだ．後者の隠れマルコフモデルについては当ブログですでに取り扱った題材のため，そちらをご覧いただきたい．
　⇒マルコフモデルと隠れマルコフモデル
それでは，動的計画法について確認していこう．

動的計画法(Dynamic Programming)とは

「Viterbiアルゴリズムは動的計画法アルゴリズムの一種」とwikipediaの概要には記載してあるが，そもそも動的計画法とは何なのだろうか．wikipediaを確認してみよう．

“動的計画法（どうてきけいかくほう、英: Dynamic Programming, DP）は、計算機科学の分野において、アルゴリズムの分類の1つである。対象となる問題を複数の部分問題に分割し、部分問題の計算結果を記録しながら解いていく手法を総称してこう呼ぶ。” – 動的計画法(wikipedia)

具体的には，以下の2条件を満たすアルゴリズムを動的計画法と呼ぶ．
◆分割統治法
分割統治法では，大きな問題を小さな問題に分割し，分割後の小さな問題をすべて解決することで最終的に大きな問題を解決する．一般的には小さな問題に分解したあと再帰によって個別に問題を解決していくが，同じ問題を複数回解決する必要がある場合などに計算コストが著しく増加する恐れがある．その問題を防ぐ方法として，もう1つの条件であるメモ化を利用する．
◆メモ化
メモ化とは，一度計算した結果を保持しておくことで同じ問題の再計算を不要とする手法である．メモ化により計算量が削減されることで，プログラムの高速化や最適化が可能となる．

動的計画法については別の記事でより詳細に解説する予定のため，今回は上記の説明にとどめる．
次に，Viterbiアルゴリズムの目的について確認しよう．

Viterbiアルゴリズムの目的

Viterbiアルゴリズムの目的は，wikipediaにも記載されている通り観測された出力から最も尤もらしい状態系列を推測することである．Viterbiアルゴリズムでは，その最も尤もらしい状態系列をビタビ経路と呼ぶ．
ご存じのとおり，隠れマルコフモデルでは状態が隠れている．Viterbiアルゴリズムでは，遷移確率と出力確率，出力結果から，その隠された状態の系列を推測することが目的となる．

それでは，Viterbiアルゴリズムによる状態系列の推定手順を確認しよう．

Viterbiアルゴリズムの推定手順

推定手順を確認する前に，いくつか変数を定義しよう．
今回，推定に用いる隠れマルコフモデルをMとし，Mの出力系列をo^T=o₁,…,o_Tとする．o^Tを出力するような状態遷移系列は複数あることが一般的であるが，その中から確率的に最も尤もらしい状態遷移系列を推定することがViterbiアルゴリズムの目的となる．これは，状態遷移系列をq^T=q₁,…,q_Tとした時，出力系列が出力される確率P(o^T,q^T|M)が最大となるような状態遷移系列q^Tを求めるということである．
時刻tで状態q_iに到達する状態遷移系列に関して，最大の確率値をδ_t(i)とする．このとき，状態毎に存在するδ_t(i)は以下の式で表される．この式の右辺はモデルMにおいて，状態q_t-1から状態q_tに遷移し，かつo_tが出力されるような状態q_t-1の中で最も高い確率値を返す．なお，式中のX_tは現在の状態を表す．

$$\delta_t (i) = \max_{q_{t-1}} P(q_{t-1},X_t=q_i,o_t|M)$$

δ_t(i)を再帰的に計算するため，Viterbiアルゴリズムでは以下の式を用いる．なお，式中のa_ijは状態q_iから状態q_jへの遷移確率，b_j(o_t+1)は状態q_jにおけるo_t+1の出力確率を表す．

$$\delta_{t+1} (j) = \max_{i} [\delta_t(i)a_{ij}]b_j(o_{t+1})$$

また，最後に状態遷移系列を復元するため，最大の確率値δ_t+1(j)を与える直前の状態をψ(･)に記憶しておく．

それでは，Viterbiアルゴリズムの推定手順について確認しよう．手順には大きく分けて「初期化」「再帰処理」「再帰終了後処理」「最適状態系列の復元」の４つの段階がある．

１．初期化

まず，t=1の時の状態q_i(i=1,2,…,N)における変数δ，ψについて以下のように初期化を行う．なお，π_iは状態q_iの初期状態確率(状態q_iが初期状態となる確率)である．このことから，δ₁(i)は，各状態q_iについて初期状態かつo₁が出力される確率となることがわかるだろう．

$$\delta_1(i)=π_ib_i(o_1)$$

$$\psi_1(i)=0$$

２．再帰処理

時刻t=1,…,T-1として，状態q_j(j=1,…,N)の最大の確率値δ_t+1(j)を再帰的に計算する．また，最大の確率値δ_t+1(j)を与える直前の状態iを記憶するψについても更新する．

$$\delta_{t+1} (j) = \max_{i} [\delta_t(i)a_{ij}]b_j(o_{t+1})$$

$$\newcommand{\argmax}{\mathop{\rm arg~max}\limits} \psi_{t+1} (j) = \argmax_{i} [\delta_t(i)a_{ij}]$$

余談だが，max[f(x)]はf(x)を最大にするxを返し，argmax[f(x)]はf(x)を最大にするxの集合を返す．

３．再帰終了後処理

再帰処理は時刻t=T-1で終了するため，最後に時刻t=Tにおける最大の確率値Pと状態遷移系列q_Tを計算する．

$${\bf P} = \max_{i} \delta_T (i)$$

$$\newcommand{\argmax}{\mathop{\rm arg~max}\limits} {\bf q_T} = \argmax_{i} \psi_t (i)$$

４．最適状態系列の復元

３．再帰終了後処理までの手順で得られた状態遷移系列q^Tについてt=T-1,…,1の順に以下の式を用いて最適状態系列を獲得する．

$${\bf q_t} = \psi_{t+1} ({\bf q_{t+1}})$$

以上が，Viterbiアルゴリズムの推定手順である．数式のみではわかりづらい部分もあると思うので，例題と図を用いて再度手順を確認してみよう．

Viterbiアルゴリズムの推定手順(例題)

それでは，Viterbiアルゴリズムの推定手順で確認した手順を，例題に当てはめて再度確認しよう．
今回，「John has fried chicken for dinner」という英文の品詞情報を推定する問題を考える．対象の英文の品詞系列(状態遷移系列)には名詞-動詞-形容詞-名詞-前置詞-名詞(訳:ジョンは夕食にフライドチキンを食べる)と名詞-動詞-動詞-名詞-前置詞-名詞(訳:ジョンは夕食のためにチキンを揚げている)の2パターンが考えられる．今回は，下図のような隠れマルコフモデルを用いて，どちらの品詞系列が尤もらしいかを確率的に求めてみよう．

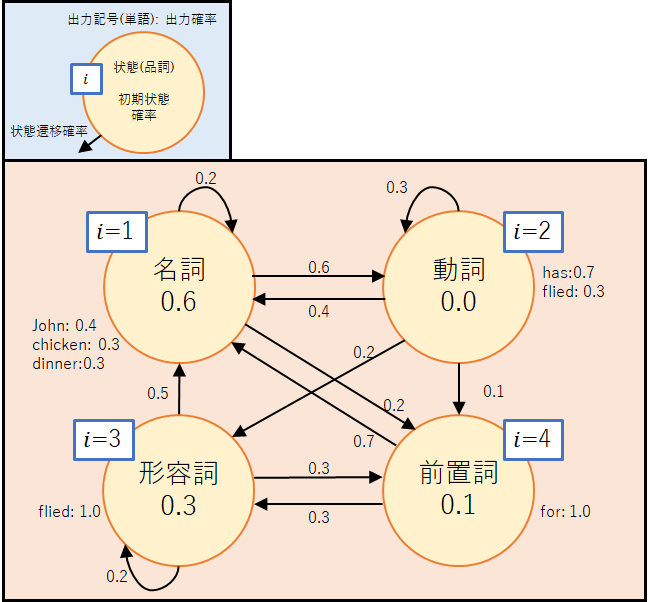
では，推定手順に沿って確認していこう．

１．初期化(例題)

まず，すべての状態q_iについて，δ₁(i)とψ₁(i)を初期化する．今回はo₁=”John”である．

$$\delta_1(i)=π_ib_i(o_1)$$

$$\psi_1(i)=0$$

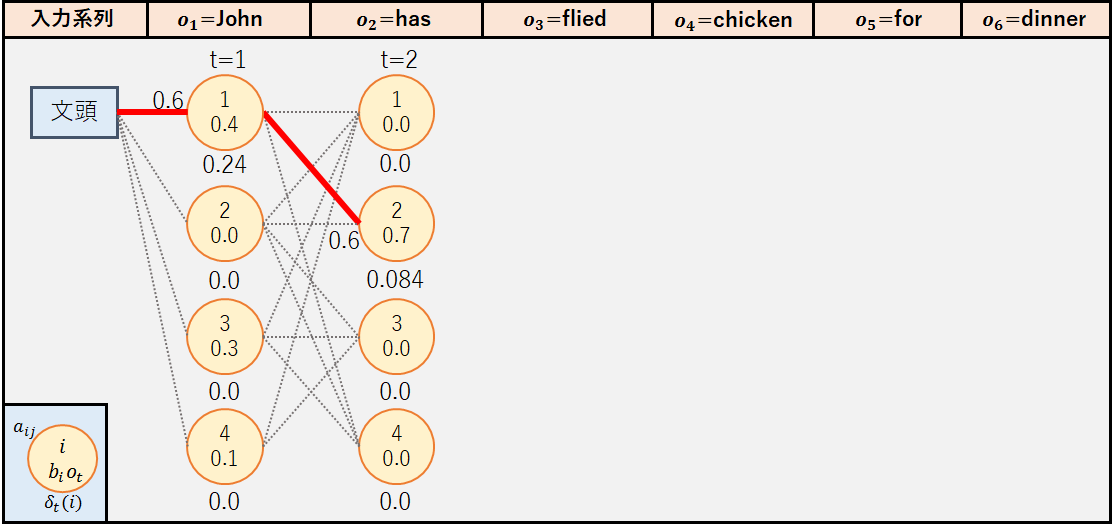
この時の経路図は以下のようになる．図中で[文頭]から状態1に伸びている赤線は，状態毎の最大の確率値をとる経路を表している．なお今回は図を見やすくするため，最大の確率値が0.0である状態へのパスについては赤線を記載していない．例えば，状態2ではo₁=”John”の出力確率が0であることから最大の確率値は0.0となるため，パスはグレーの点線となっている．

２．再帰処理(例題)

初めに，今回の例題で再帰処理を行った後の経路図を載せておく．つまり，手順通りに経路を推定した場合，状態遷移系列q^Tは{1,2,3,1,4,1}=名詞-動詞-形容詞-名詞-前置詞-名詞となるはずである．それでは，手順に沿って経路図を作成してみよう．

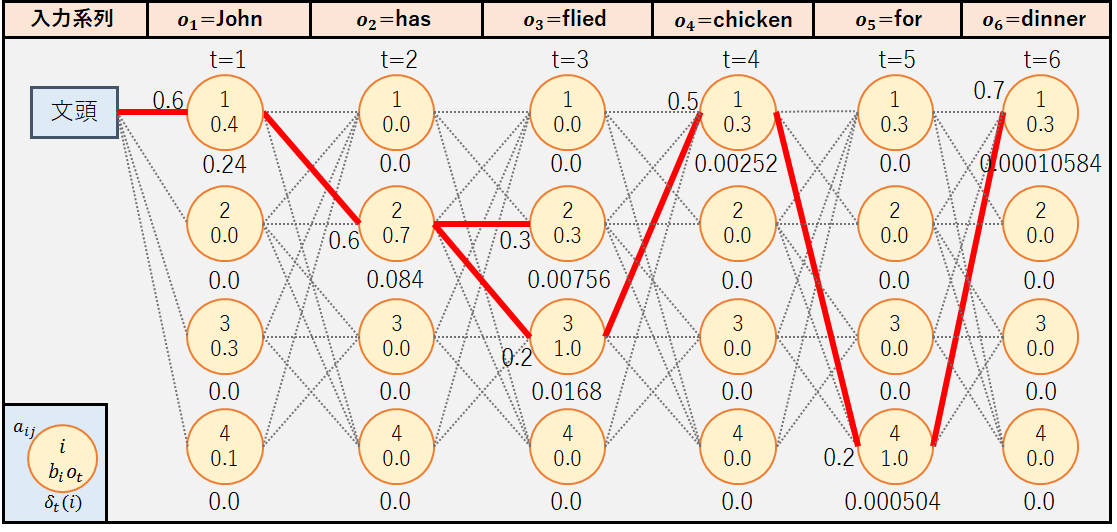
①t=1(o₂=”has”)

今回は簡略化のため，最大の確率値が0.0である状態についてはψ_t(j)を保持しないこととする．

　◆j=1
　　出力確率b₁(o₂)が0のため，δ₂(1)=0.0
　◆j=2

$$\delta_2(2)=[\delta_1(1)a_{12}]b_2(o_2)=0.24・0.5・0.7=0.084$$

$$\psi_2(2) = \{1\}$$

　◆j=3
　
　　出力確率b₃(o₂)が0のため，δ₂(3)=0.0
　◆j=4
　　出力確率b₄(o₂)が0のため，δ₂(4)=0.0

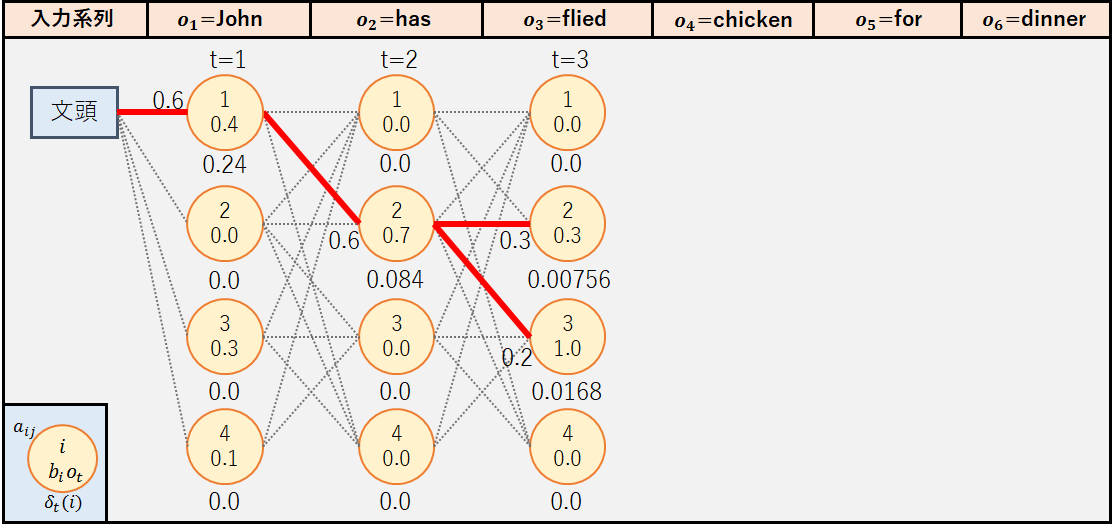
②t=2(o₃=”fried”)

　◆j=1
　　出力確率b₁(o₃)が0のため，δ₃(1)=0.0
　◆j=2

$$\delta_3(2) = \max_{i} [\delta_2(i)a_{i2}]b_2(o_3) = [\delta_2(2)a_{22}]b_2(o_3) = 0.084・0.3・0.3 = 0.00756$$

$$\psi_3(2) = \{2\}$$

　◆j=3

$$\delta_3 (3) = \max_{i} [\delta_2(i)a_{i3}]b_3(o_3) = [\delta_2(2)a_{23}]b_3(o_3) = 0.084・0.2・1.0 = 0.0168$$

$$\psi_3 (3) = \{2\}$$

　◆j=4
　　出力確率b₄(o₃)が0のため，δ₃(4)=0.0

③t=3(o₄=”chicken”)

　◆j=1

$$\delta_4(1) = \max_{i} [\delta_3(i)a_{i1}]b_1(o_4) = [\delta_3(3)a_{31}]b_1(o_4) = 0.0168・0.5・0.3 = 0.00252$$

$$\psi_4(1) = \{3\}$$

　◆j=2
　　出力確率b₂(o₄)が0のため，δ₄(2)=0.0
　◆j=3
　　出力確率b₃(o₄)が0のため，δ₄(3)=0.0
　◆j=4
　　出力確率b₄(o₄)が0のため，δ₄(4)=0.0

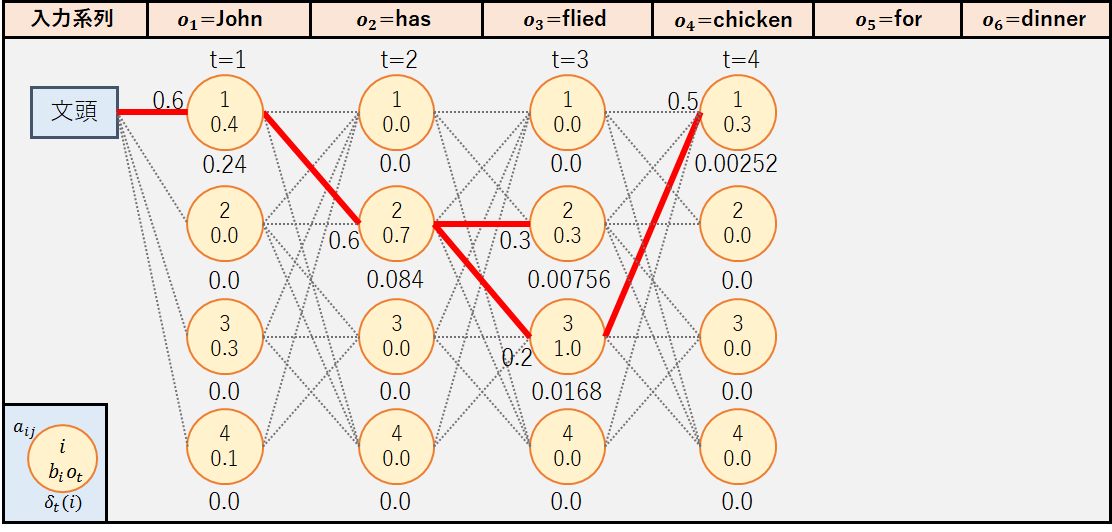
ここで注目してほしいのは，状態q₂ではなく状態q₃からのパスが採用された点である．これはo₃=”fried”が動詞よりも形容詞である確率が高いと推定されたことを表している．

④t=4(o₅=”for”)

　◆j=1
　　出力確率b₁(o₅)が0のため，δ₅(1)=0.0
　◆j=2
　　出力確率b₂(o₅)が0のため，δ₅(2)=0.0
　◆j=3
　　出力確率b₃(o₅)が0のため，δ₅(3)=0.0
　◆j=4

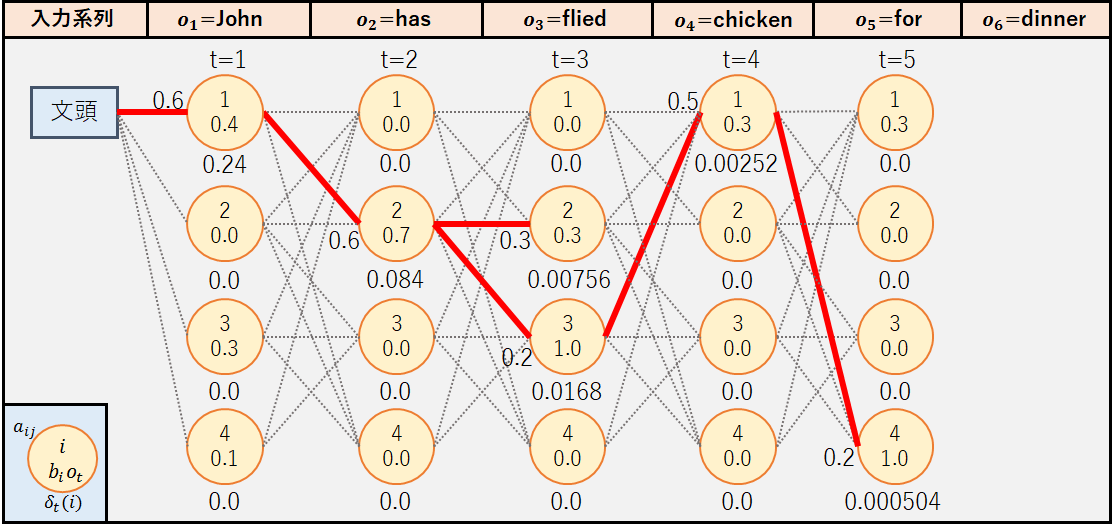
$$\delta_5(4) = \max_{i} [\delta_4(i)a_{i4}]b_4(o_5) = [\delta_4(1)a_{14}]b_4(o_5) = 0.00252・0.2・1.0 = 0.000504$$

$$\psi_5(4) = \{1\}$$

⑤t=5(o₆=”dinner”)

　◆j=1

$$\delta_6(1) = \max_{i} [\delta_5(i)a_{i1}]b_1(o_6) = [\delta_5(4)a_{41}]b_1(o_6) = 0.000504・0.7・0.3 = 0.00010584$$

$$\psi_6(1) = \{4\}$$

　◆j=2
　　出力確率b₂(o₆)が0のため，δ₆(2)=0.0
　◆j=3
　　出力確率b₃(o₆)が0のため，δ₆(3)=0.0
　◆j=4
　　出力確率b₄(o₆)が0のため，δ₆(4)=0.0

３．再帰終了後処理(例題)

２．再帰処理(例題)でt=T-1=5まで再帰処理を行ったため，t=T=6における最大の確率値Pと状態系列q_Tを計算する．

$${\bf P} = \max_{i} \delta_T (i) = \delta_6 (1) = 0.00010584$$

$$\newcommand{\argmax}{\mathop{\rm arg~max}\limits} {\bf q_6} = \argmax_{i} \psi_t (i) = \psi_6 (1) = \{1\}$$

４．最適状態系列の復元(例題)

最後に，t=6,5,4,3,2,1として最適状態系列をバックトラックによって復元する．

$${\bf q_5} = \psi_6 ({\bf q_6}) = \psi_6 (1) = 4$$

$${\bf q_4} = \psi_5 ({\bf q_5}) = \psi_5 (4) = 1$$

$${\bf q_3} = \psi_4 ({\bf q_4}) = \psi_4 (1) = 3$$

$${\bf q_2} = \psi_3 ({\bf q_3}) = \psi_3 (3) = 2$$

$${\bf q_1} = \psi_2 ({\bf q_2}) = \psi_2 (2) = 1$$

よって，最適状態系列q^T(t=1,2,3,4,5,6)は以下の通りとなる．

$${\bf q^T} = \{q_t|t=1,2,3,4,5,6\} = \{1,2,3,1,4,1\}$$

この結果は，今回の隠れマルコフモデルで推定した結果，品詞系列名詞-動詞-形容詞-名詞-前置詞-名詞(訳:ジョンは夕食にフライドチキンを食べる)の方が尤もらしいと推定されたことを表している．もちろん，別の隠れマルコフモデルを用いて推定した場合に結果が変わることもある．ここで重要となるのは隠れマルコフモデルのパラメータ(遷移確率，出力確率)であるが，それらの決定には出力系列からモデルのパラメータを推定するバウム・ウェルチアルゴリズムが用いられる(説明は割愛)．

以上で，Viterbiアルゴリズムによる推定の手順の解説は終了である．最後に，Viterbiアルゴリズムの応用可能性について確認しよう．

Viterbiアルゴリズムの応用可能性

Viterbiアルゴリズムはどのような分野で応用できるのであろうか．応用分野のひとつに自然言語処理分野が挙げられる．本解説の導入でも述べた通り，Viterbiアルゴリズムは形態素解析器であるMeCab，Chasen，JUMANで解探索アルゴリズムとして採用されている．複数の解釈があり得る自然言語を形態素ごとに分解し品詞情報を付加する場合，複数の分解パターンを確率的に比較することができる．
その他にも，音声処理分野や文字認識分野でもViterbiアルゴリズムによる推定は大いに貢献している．

参考

【論文】
・Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm
・The Viterbi Algorithm
【書籍】
・北研二:言語と計算ー４　確率的言語モデル(1999)．

【Webサイト】
・ビタビアルゴリズム – wikipedia
・動的計画法 – wikipedia
・分割統治法 – wikipedia
・メモ化 – wikipedia
・ビタビアルゴリズム【入門】具体例で分かりやすく解説！（Viterbi）
・隠れマルコフモデル（HMM）について
・HMM viterbi
・2009 Open Campus No.3 言コミ報告＜体験授業x3＞！(8/2)

人工知能・機械学習・自然言語処理周辺の技術情報

目次