動的計画法がわかる！ダイクストラ法の実装(Python)や問題への適用手順

執筆：金子冴

今回は，Viterbiアルゴリズムの解説(【技術解説】HMMに基づいたViterbiアルゴリズムによる解推定手法(例題つき))をした際に登場した動的計画法について，その解説と，簡単な例を用いたプログラム(Python)での実装例を紹介する．また，問題文から動的計画法を用いて問題を解決する際のプロセス(漸化式の作成方法等)についても触れながら，具体的な応用方法について確認する．まずは，動的計画法とはどういうものなのか，概要を確認しよう．

動的計画法(DP;Dynamic Programming)とは

動的計画法の概要

動的計画法とはそのままでは解けないような大きな問題を複数の小さな問題(部分問題と呼ぶ)に分解し，部分問題を解くことで元の大きな問題を解く手法の総称である．動的計画法を用いることで多項式時間で解くことができない一部の問題について，類似多項式時間で最適解を求めることができる(後ほど解説)．問題のある手法が動的計画法であるかどうかを判断する際には，分割統治法とメモ化の2つを満たしているかどうかが条件となる．はじめに，多項式時間，分割統治法，メモ化について理解しよう．

多項式時間，多項式時間アルゴリズムとは

多項式時間とは多項式で表される計算時間を指し，多項式時間アルゴリズムとは入力サイズ(長さや個数)をnとした時，計算時間(ステップ数)の上界がnの多項式時間で表現できるアルゴリズムを指す．例えば，九九を計算するアルゴリズムの計算時間は9×9で計算できる．これをn×nに拡張した場合の計算時間のオーダーは”O”記法を用いてO(n²)と表される．これは，この計算時間の上界がn²で表現できることを指しているため，n×nの掛け算を計算するアルゴリズムは多項式時間アルゴリズムであるといえる．

しかし，多項式時間で解けない問題も存在する．例えば，今回の解説でも取り上げる最短経路問題は多項式時間で解くことはできない．図のような重み付き経路について，STARTからGOALに最短コストで到着する経路を求める問題を考えてみよう．
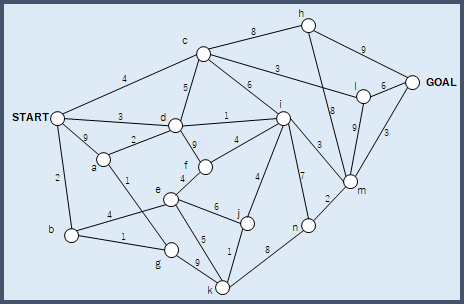最短経路を求めるためには全経路の組み合わせを考慮した上でSTARTからGOALまでのコストを計算し，コストが最小の経路を選択する必要がある．このような問題では入力サイズが増えていく毎に経路パターンが指数的に増加していくため，全経路のコストを計算する手法は現実的ではない．しかし，動的計画法を使用することで，最短経路問題のような多項式時間で解けない問題の最適解を解ける場合がある．その計算時に使用するのが分割統治法とメモ化という2つの手法である．

分割統治法とは

分割統治法とは対象の問題を部分問題に分割する手法を指す．では，先ほど挙げた最短経路問題を部分問題に分解してみよう．今回の例では，まずSTARTからENDの全経路を考えるのではなく，ある時点から進むことができる経路のみを考えるというアプローチをとることとする．すると，初めの経路はSTARTからa, b, c, dの4本のみ考えればよいことになる．最短経路問題を解くことを考えると，ここではSTARTから最も低いコストで遷移できるSTART→bを選択しよう．

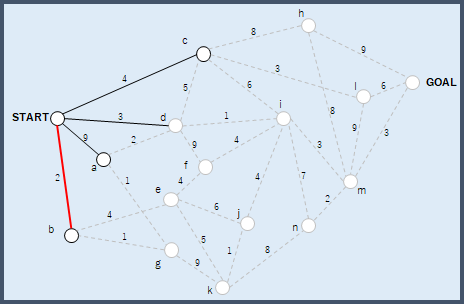
次は，bから進むことができる経路のみを考え，ここでも最もコストが低い経路を選択する．今回の例ではb→gを選択することになる．

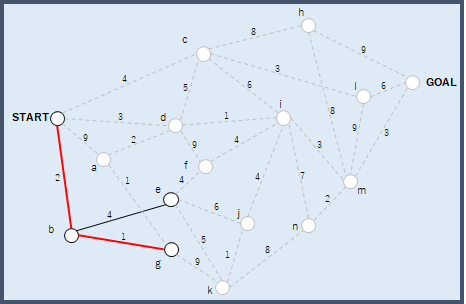
このように全経路を考える問題をある時点から進むことができる経路のみを考える問題(部分問題)に分割するような手法を分割統治法と呼ぶ．

メモ化とは

メモ化とは計算結果をメモリ上などに保持し，あとから再利用する手法を指す．メモ化の例として，フィボナッチ数列を計算する問題を考えてみよう．フィボナッチ数列についての説明は割愛する．フィボナッチ数列をPythonで計算する場合，通常は以下のようなコードになる．

CulcFibonacci.py

import sys

# フィボナッチ数の計算
def culc_fibonacci(n):
	if n > 1:
		return culc_fibonacci(n-1) + culc_fibonacci(n-2)
	elif n == 1:
		return 1
	else:
		return 0

def main():
	# 1～10番目フィボナッチ数列を表示
	# 	⇒　0, 1, 1, 2, 3, 5, 8, 13, 21, 34
	for n in range(10):
		fibonacci_n = culc_fibonacci(n)
		print(fibonacci_n, end='')
		if not  n == 9:
			print(', ', end='')


if __name__ == '__main__':
	main()
	sys.exit(0)

import sys

# フィボナッチ数の計算

def culc_fibonacci(n):

if n > 1:

return culc_fibonacci(n-1) + culc_fibonacci(n-2)

elif n == 1:

return 1

else:

return 0

def main():

# 1～10番目フィボナッチ数列を表示

# ⇒　0, 1, 1, 2, 3, 5, 8, 13, 21, 34

for n in range(10):

fibonacci_n = culc_fibonacci(n)

print(fibonacci_n, end='')

if not n == 9:

print(', ', end='')

if __name__ == '__main__':

main()

sys.exit(0)

しかし，このコードではn=10を計算するために，再度n=9~1までの計算をする必要があり，計算時間はO(αⁿ)(α:実数)となるため，nが大きくなるにつれて計算量が指数的に増加していく．

以下の図はフィボナッチ数列の計算を表している．図から，f(10)以外のフィボナッチ数は2回以上計算されることがわかるだろう．

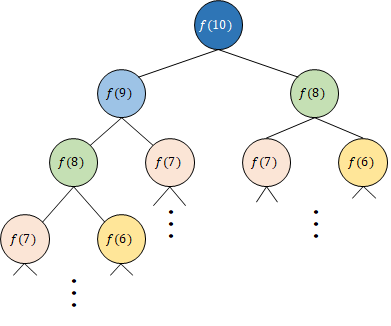
このコードをメモ化によって最適化する際には，複数回計算される点が重要となる．メモ化をするためにメモ化テーブルを作成し，1度計算した値はメモ化テーブルに保持してみよう．

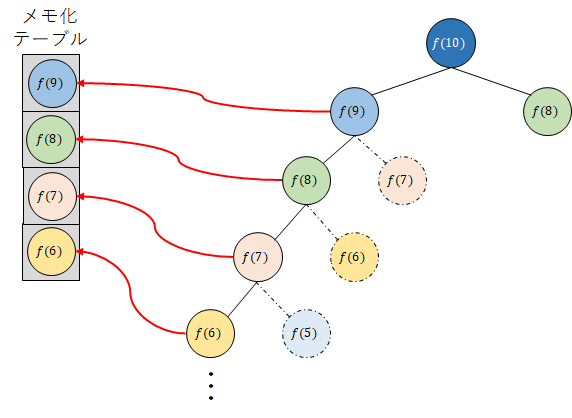
そして，再度計算に使用する際は，再計算するのではなく，メモ化テーブルから値を取得する．これにより，同じ計算の複数回実行を防ぐことができる．

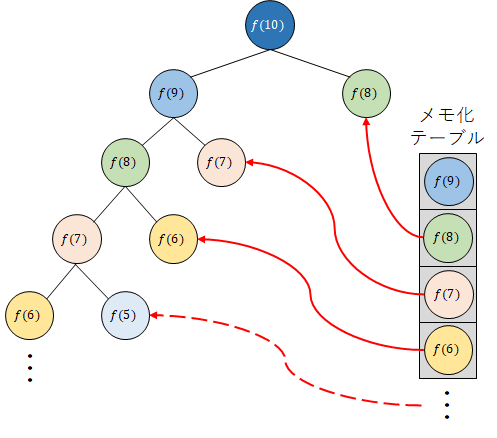
以下のソースコードは，前述のフィボナッチ数列に対してメモ化を適用したソースコードである．

CulcFibonacciMemo.py

import sys

# メモ化テーブル(辞書形式)
fibonacci_list = {}

# フィボナッチ数の計算(メモ化あり)
def culc_fibonacci_memo(n):
	global fibonacci_list
	if n == 1:
		return 1
	elif n == 0:
		return 0
	if not n in fibonacci_list:
		fibonacci_list[n] = culc_fibonacci_memo(n-1) + culc_fibonacci_memo(n-2)
	return fibonacci_list[n]

def main():
	# 1～10番目フィボナッチ数列を表示
	# 	⇒　0, 1, 1, 2, 3, 5, 8, 13, 21, 34
	for n in range(10):
		fibonacci_n = culc_fibonacci_memo(n)
		print(fibonacci_n, end='')
		if not  n == 9:
			print(', ', end='')

if __name__ == '__main__':
	main()
	sys.exit(0)

import sys

# メモ化テーブル(辞書形式)

fibonacci_list = {}

# フィボナッチ数の計算(メモ化あり)

def culc_fibonacci_memo(n):

global fibonacci_list

if n == 1:

return 1

elif n == 0:

return 0

if not n in fibonacci_list:

fibonacci_list[n] = culc_fibonacci_memo(n-1) + culc_fibonacci_memo(n-2)

return fibonacci_list[n]

def main():

# 1～10番目フィボナッチ数列を表示

# ⇒　0, 1, 1, 2, 3, 5, 8, 13, 21, 34

for n in range(10):

fibonacci_n = culc_fibonacci_memo(n)

print(fibonacci_n, end='')

if not n == 9:

print(', ', end='')

if __name__ == '__main__':

main()

sys.exit(0)

メモ化の最大のメリットは計算量が減ることで計算時間を削減できることである．このソースコードでは一度計算したフィボナッチ数をリストに格納しておき，あとで再利用することで計算量を減らす試みがされている．実際に著者のPCで40番目のフィボナッチ数を計算した際の計算時間を比較すると，前者のメモ化なしプログラムでは101.9秒だったのに対して，後者のメモ化ありプログラムでは0.2秒と大幅に計算時間が短縮されていた．動的計画法では部分問題を再帰的に計算するため，このメモ化による最適化が大きな意味を持つ．

それでは，動的計画法の概要についてはここまでとし，次は最短経路問題を動的計画法の一種であるダイクストラ法で解いてみよう．

例題：最短経路問題をダイクストラ法で解く(Python実装)

ダイクストラ法は最短経路問題を効率よく解く手法である．今回は『分割統治法とは』の項で使用したものより簡単な以下のグラフを用いて計算手順を確認しよう．

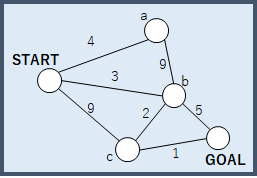
ダイクストラ法の計算手順

まずSTARTから伸びるエッジでつながるノード(a, b, c)についてSTARTからの最短経路を求める．今回の例ではSTARTから伸びるエッジでつながるノードのうち，ノードbが最小コスト3で遷移可能であることがわかる．また，STARTから別のノードを経由してbにたどり着いても，負のコストがない限り，他ノード経由の経路はSTART→bの経路よりコストが高くなることがわかるだろう．そのためSTARTからノードbへの最短経路はSTART→bと確定できる．

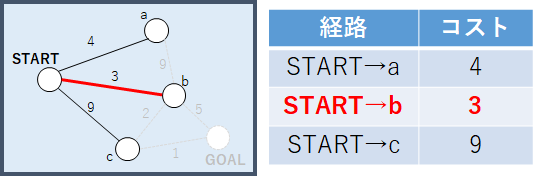
次に先ほど確定したノードbからたどり着けるノードa, c, GOALについて最小コストを求める．ここでノードbにたどり着くまでのコストは3で確定していることに注意してほしい．また，ここで注目すべきはノードaとノードcには，ノードb以外にSTARTからもエッジが伸びていることである．そのためSTARTから各ノードへの最短経路はSTARTからの最短距離とノードbからの最短経路のうち，コストが低い経路となる．これらを踏まえて計算すると，先ほど確定したノードbから各ノード(a, c, GOAL)へ遷移する最小コストはノードaが4，ノードcが5，ノードGOALが8となる．ここから，先ほどと同様に最小コストで遷移できるノードを確定するとノードaが確定される．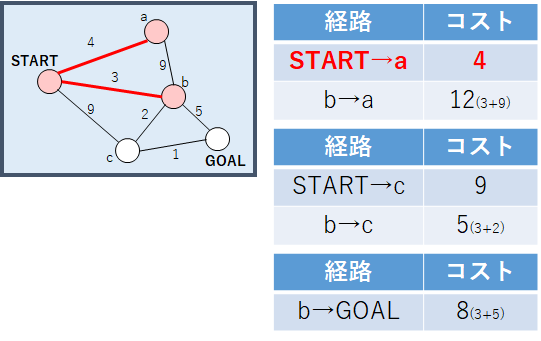

手順に従い，次に先ほど確定したノードaについて遷移可能なノードから最小コストのノードを選ぶ．しかし，ノードaから遷移可能なノードSTART, bはどちらもすでに最小コストが確定している．そのため，先ほどノードaの次に小さいコストで遷移可能であったノードcを確定としノードcからたどり着けるノード(GOALのみ)について最小コストを求める．お分かりのとおり，STARTからノードcへの最小コストは5と確定しているため，ノードGOALへ遷移するコストは6となり，ノードGOALが確定する．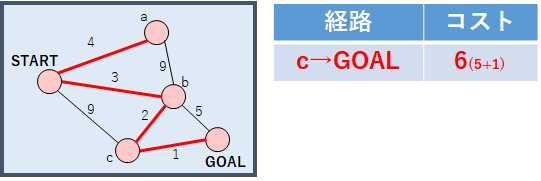

ノードGOALが確定した時点で，ダイクストラ法の計算は終了である．最後にノードSTARTからノードGOALへの最短経路(最小コストで遷移可能な経路)を考えよう．これまでの計算でノードGOALにたどり着く経路は「START→b→GOAL(コスト8)」と「START→b→c→GOAL(コスト6)」の2通りがあることがわかっている．もうお分かりのとおりノードSTARTからノードGOALへの最短経路は「START→b→c→GOAL(コスト6)」となる．

上記の手順のプログラム(python)実装の一例を以下に記載する．

edge_inf.csv

START,a,4
START,b,3
START,c,9
a,b,9
b,c,2
b,GOAL,5
c,GOAL,1

START,a,4

START,b,3

START,c,9

a,b,9

b,c,2

b,GOAL,5

c,GOAL,1

culc_dijkstra.py

import sys
import re
import heapq

# グラフの初期化
def initialize_graph():
	graph = {}
	edge_list = read_file()
	for edge_inf in edge_list:
		node1 = edge_inf.split(',')[0]
		node2 = edge_inf.split(',')[1]
		cost = int(edge_inf.split(',')[2])
	    # ノードの設定と無向エッジのコスト設定
		graph = set_new_node(graph, node1, node2)
		graph[node1][node2] = cost
		graph[node2][node1] = cost
	return graph

def read_file():
	file_name = 'edge_inf.csv'
	edge_list = []
	with open(file_name,'r',encoding='utf-8') as fin:
		for line in fin.readlines():
			edge_list.append(re.sub(r'[\r\n]','',line))
	return edge_list

def set_new_node(graph, node1, node2):
	if not node1 in graph.keys():
		graph[node1] = {}
	if not node2 in graph.keys():
		graph[node2] = {}
	return graph

# ダイクストラ法によって最短経路問題を解く
def solve_by_dijkstra(graph):
	# ノード毎のSTARTからの最小コスト
	min_dist_dict = {}
	# ノードに最小コストで辿り着く場合の直前のノード
	prev_node_dict = {}
	q = []
	heapq.heappush(q, (0, 'START'))
	
	prev_node = ''

	while True:
		# 確定したノードから遷移可能なノードのうち
		# 最小のコストと遷移先ノードをmin_dist_dictとprev_node_dictに設定
		dist, node = heapq.heappop(q)
		min_dist_dict[node] = dist
		prev_node_dict[node] = prev_node
		# もしGOALノードの最小コストが確定したらループを抜ける
		if node == 'GOAL': 
			return min_dist_dict, prev_node_dict
		prev_node = node
		# 確定したノードから遷移可能なノードについて
		# コストを計算し，キュー(q)に追加する
		culc_min_dist_and_put(graph, q, node, min_dist_dict, prev_node_dict)

def culc_min_dist_and_put(graph, q, departure_node, min_dist_dict, prev_node_dict):
	# 直前に確定したノードから遷移可能なすべてのノードについて繰り返し
	for arrival_node in graph[departure_node].keys():
		# 遷移可能なノードについて，直前に確定したノードから遷移した場合のコストを計算
		tmp_d = min_dist_dict[departure_node] + graph[departure_node][arrival_node]
		# 過去に遷移先ノードの最小コストを計算済みかどうか
		if arrival_node in min_dist_dict.keys():
			# 過去に計算していたSTARTからの最小コストより直前に確定したノードから遷移した場合の
			# コストが小さかった場合，最小コストを更新
			if tmp_d < min_dist_dict[arrival_node]:
				min_dist_dict[arrival_node] = tmp_d
				heapq.heappush(q, (min_dist_dict[arrival_node], arrival_node))
		else:
			min_dist_dict[arrival_node] = tmp_d
			heapq.heappush(q, (min_dist_dict[arrival_node], arrival_node))

def main():
	graph = initialize_graph()
	min_dist_dict, prev_node_dict = solve_by_dijkstra(graph)
	# GOALノードからprev_node_dictをたどって経路を復元
	print('Route : GOAL ',end='')
	node = 'GOAL'
	while True:
		if node == 'START':
			print()
			break
		print(' ← ' + prev_node_dict[node],end='')
		node = prev_node_dict[node]
#	⇒Route : GOAL  ← c ← a ← b ← START
	print('Min Cost : ' +  str(min_dist_dict['GOAL']))
#	⇒Min Cost : 6

if __name__ == '__main__':
	main()
	sys.exit(0)

import sys

import re

import heapq

# グラフの初期化

def initialize_graph():

graph = {}

edge_list = read_file()

for edge_inf in edge_list:

node1 = edge_inf.split(',')[0]

node2 = edge_inf.split(',')[1]

cost = int(edge_inf.split(',')[2])

# ノードの設定と無向エッジのコスト設定

graph = set_new_node(graph, node1, node2)

graph[node1][node2] = cost

graph[node2][node1] = cost

return graph

def read_file():

file_name = 'edge_inf.csv'

edge_list = []

with open(file_name,'r',encoding='utf-8') as fin:

for line in fin.readlines():

edge_list.append(re.sub(r'[\r\n]','',line))

return edge_list

def set_new_node(graph, node1, node2):

if not node1 in graph.keys():

graph[node1] = {}

if not node2 in graph.keys():

graph[node2] = {}

return graph

# ダイクストラ法によって最短経路問題を解く

def solve_by_dijkstra(graph):

# ノード毎のSTARTからの最小コスト

min_dist_dict = {}

# ノードに最小コストで辿り着く場合の直前のノード

prev_node_dict = {}

q = []

heapq.heappush(q, (0, 'START'))

prev_node = ''

while True:

# 確定したノードから遷移可能なノードのうち

# 最小のコストと遷移先ノードをmin_dist_dictとprev_node_dictに設定

dist, node = heapq.heappop(q)

min_dist_dict[node] = dist

prev_node_dict[node] = prev_node

# もしGOALノードの最小コストが確定したらループを抜ける

if node == 'GOAL':

return min_dist_dict, prev_node_dict

prev_node = node

# 確定したノードから遷移可能なノードについて

# コストを計算し，キュー(q)に追加する

culc_min_dist_and_put(graph, q, node, min_dist_dict, prev_node_dict)

def culc_min_dist_and_put(graph, q, departure_node, min_dist_dict, prev_node_dict):

# 直前に確定したノードから遷移可能なすべてのノードについて繰り返し

for arrival_node in graph[departure_node].keys():

# 遷移可能なノードについて，直前に確定したノードから遷移した場合のコストを計算

tmp_d = min_dist_dict[departure_node] + graph[departure_node][arrival_node]

# 過去に遷移先ノードの最小コストを計算済みかどうか

if arrival_node in min_dist_dict.keys():

# 過去に計算していたSTARTからの最小コストより直前に確定したノードから遷移した場合の

# コストが小さかった場合，最小コストを更新

if tmp_d < min_dist_dict[arrival_node]:

min_dist_dict[arrival_node] = tmp_d

heapq.heappush(q, (min_dist_dict[arrival_node], arrival_node))

else:

min_dist_dict[arrival_node] = tmp_d

heapq.heappush(q, (min_dist_dict[arrival_node], arrival_node))

def main():

graph = initialize_graph()

min_dist_dict, prev_node_dict = solve_by_dijkstra(graph)

# GOALノードからprev_node_dictをたどって経路を復元

print('Route : GOAL ',end='')

node = 'GOAL'

while True:

if node == 'START':

print()

break

print(' ← ' + prev_node_dict[node],end='')

node = prev_node_dict[node]

# ⇒Route : GOAL ← c ← a ← b ← START

print('Min Cost : ' + str(min_dist_dict['GOAL']))

# ⇒Min Cost : 6

if __name__ == '__main__':

main()

sys.exit(0)

最短経路問題を解く手法の1つであるダイクストラ法については理解いただけただろうか．しかし，ダイクストラ法のように確立した手法で解ける問題以外に対しては，どのように動的計画法を当てはめるべきなのだろうか．それでは，実際にある問題を動的計画法で解く際の解決手順について考えていこう．

動的計画法を用いた問題解決手順

それでは初めにある問題が出されたとき，動的計画法を当てはめ，解決するまでの手順について解説する．

動的計画法を用いる場合の解決手順

①全探索が可能かどうかを確認

まず，ある問題が与えられた場合にその問題が全探索で解けるスケールかどうかを考える．一般的に，全探索することで最適解が求まることは先ほどまでの解説で理解いただけただろう．また同時に，入力サイズが大きくなった場合に全探索の計算時間が膨大になることについても確認済みである．動的計画法を当てはめる際には初めに全探索が可能かを確認し，全探索が可能であれば動的計画法を用いないことが賢明である．なぜならば，動的計画法で最適解が求められるとは限らないからである．全探索が可能であれば，全探索で正しい最適解を求めることが望まれる．なお，全探索は可能だが短時間で計算したい場合やメモリ使用量を抑えたい場合などは，動的計画法を使用することも選択肢に含めると良い．
ここでは，全探索が実用的に不可能であり，動的計画法で最適解を求めることを考え，次の手順に進もう．

②部分問題に分割可能かどうかを確認

全探索が可能かを確認した後，今度は部分問題に分割可能かどうかを確認する．これは，動的計画法と呼ばれる条件の1つである分割統治法が適用可能かを考えることと同義である．例えば，先ほど例に挙げていた最短経路問題ではSTARTからGOALまでの経路を求める問題をノード毎の最短経路を求める部分問題に分割した．部分問題に分割することで，そのままでは解けない大きな問題を解くことができるようになる．ただし部分問題に分割した結果，大きな問題が解けることが最低条件である．

③求める状態(パラメータ)を列挙

ここからは具体例なしでの理解は難しいため，最短経路問題を例に説明していく．部分問題に分割した後は，求めたい値を計算するにあたって必要となる状態(パラメータ)を列挙する．最短経路問題でいうところのSTARTから各ノードへの最小コストとどのノードから遷移してきたかが状態(パラメータ)にあたる．まとめると，最短経路問題の場合の求める対象はSTARTからGOALへの最短経路，求める状態はSTARTから各ノードへの最小コストと遷移元ノードとなる．

④メモ化のための配列を用意

分割統治法の導入と状態の列挙ができたら，動的計画法のもう1つの条件であるメモ化で使用する配列を用意する．配列の次元数は状態の個数と同じになるため，最短経路問題の場合は1次元(各ノードでのSTARTからの最短距離)となるため，例えばメモ化配列をdpとするとdp[ノード]=最小コストという形で管理することになる．このようにメモ化配列を用意することで，何度もSTARTからの最小コストを計算する必要がなくなり，計算量を削減することができる．

⑤漸化式を作成

次は，メモ化配列から漸化式を作成する．漸化式とはあるステップから次のステップを計算する際に使用する式である．漸化式の例として，フィボナッチ数列を考えてみよう．フィボナッチ数列は，直前とその前の数字を足した数列であるが，それを数式で表すと以下のようになる．

$$\begin{eqnarray}\left\{\begin{array}{l} F(x)=F(x-1)+F(x-2)\\ F(1)=1, F(0)=0 \end{array} \right. \end{eqnarray}$$

この式のように，ある項がそれ以前の項から計算できる式を漸化式と呼ぶ．動的計画法ではこのような漸化式を作成し，再帰的に計算しながら部分問題を解くことで最終的に大きな問題を解く．漸化式が完成したらあとはプログラムに落とし込むだけだが部分問題を再帰的に解き，その過程はメモ化配列に格納することを意識すれば特に問題なくコーディングできるだろう．

以上で，動的計画法の解説は終わる．今回学習した内容を実践したい場合は，AtCoderで公開されている過去問などに取り組むと良いだろう．

参考

【Webサイト】・動的計画法 – wikipedia ・多項式時間 – wikipedia ・最短経路問題・アルゴリズム入門(3)(分割統治法) ・メモ化・情報科学シケスラ　Fibonacci ・フィボナッチ数の計算と計算量・漸化式を用いた動的計画法の関数の作り方・典型的なDP(動的計画法)のパターンを整理Part1～ナップサックDP編～

人工知能・機械学習・自然言語処理周辺の技術情報

目次

動的計画法(DP;Dynamic Programming)とは

動的計画法の概要

多項式時間，多項式時間アルゴリズムとは

分割統治法とは

メモ化とは

例題：最短経路問題をダイクストラ法で解く(Python実装)

ダイクストラ法の計算手順

動的計画法を用いた問題解決手順

動的計画法を用いる場合の解決手順

参考

関連記事はこちら