【技術解説】bi-gramマルコフモデル

執筆：金子冴

今回は，形態素解析器の1つであるMeCab内で解析モデルとして用いられているbi-gram マルコフモデルについて解説する．

初めに，bi-gramの元となっている，N-gramという手法を解説しよう．

N-gramとは

N-gramの概要

「N-gram」とは，自然言語処理分野で用いられる手法の１つである．N-gramでは対象となる文書を文字単位の記号列と考え，隣接したN個の記号毎の出現頻度(度数と呼ぶ)を集計する．
隣接した1個の記号からなる記号列(つまり，1文字)毎の度数をuni-gram，2個の記号をbi-gram，3個の記号ならをtri-gram,…と呼ぶ．

N-gramを使用するメリット(形態素解析との比較)

N-gramで文書を分割すると，どのようなメリットがあるのだろうか．主なメリットとして，文法情報を用いずに文書を分解できることが挙げられる．
【技術解説】形態素解析とMeCabのアルゴリズム内で解説した形態素解析では辞書に含まれる品詞情報を元に文書を形態素毎に分解した．この方法の場合，言語に応じた辞書が必要となる．
N-gramを使用した場合，文法情報を用いずに文書を分解できるため，言語に依存しない文書の分割が可能となる．また，言語学的に意味を持たない記号列についても集計が可能なため，テキスト処理を含む自然言語処理分野では多く用いられている．

N-gramの計算例とアルゴリズム(python実装)

N-gramの計算例

例文として「きしゃがきしゃにきしゃできしゃした(記者が貴社に汽車で帰社した)」を用いて，N-gramをN=1から3まで実際に計算してみよう．
計算したuni-gram，bi-gram，tri-gramは以下のとおりになる．なお，相対頻度は記号列毎の度数を全記号列の度数の合計で割った値である．

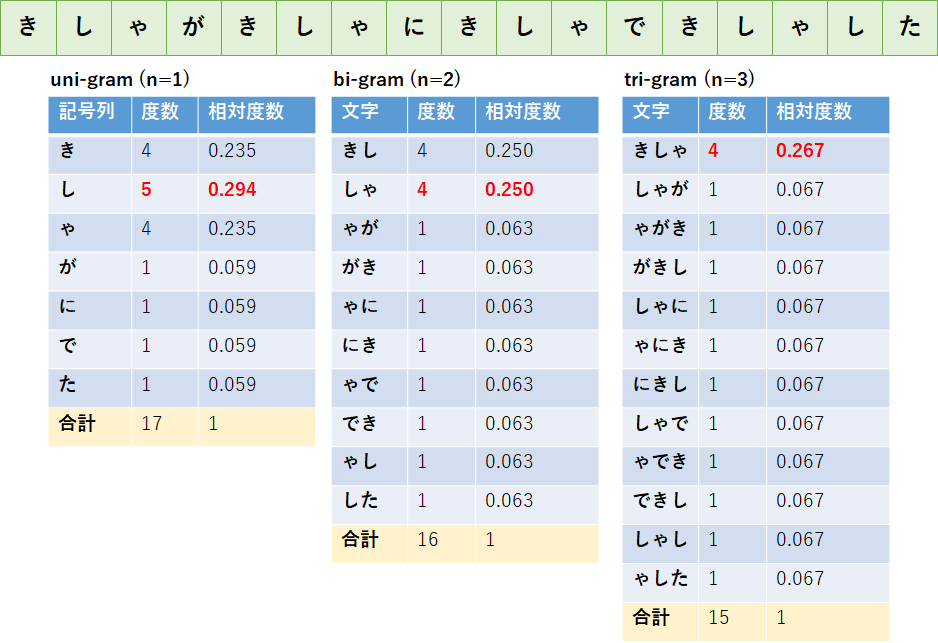
まず，隣接した1個の記号毎の度数であるuni-gram(N=1)を見てみよう．
この結果から，「きしゃ」の出現頻度が高いことがわかる．しかし，1文字単位で区切るとそれぞれの記号列が意味を持たなくなるほか，文章が多くなるにつれて助詞に該当する文字の出現頻度も比例的に増加すると推測できる．
ある程度意味のある記号列毎の度数が計算でき，文章の数が増えることによる助詞の出現頻度の増加の影響を受けにくいNの値はないだろうか．

次に，bi-gram(N=2)の結果を確認しよう．
隣接した記号の個数を2個としたことにより，文書の数が増えることで助詞の出現頻度が比例的に増加する問題は軽減できると見込まれる．
しかし，「きし」や「しゃ」など，想定とは異なる分割がされているようだ．これでは，まだ意味のある記号列毎の度数が計算できているとは言えないだろう．

最後に，tri-gram(N=3)の結果を確認しよう．
隣接した記号の個数を3個としたことにより，bi-gramの時よりも，文書の数が増えることで助詞の出現頻度が比例的に増加する問題はさらに軽減できると見込まれる．
また，tri-gramでは「きしゃ」という意味のある単語について分割がされているようだ．一般に，日本語の文章を分割する際はN=3であるtri-gramを採用する場合が多い．

N-gramの計算アルゴリズム(python実装)

今回は『N-gramの計算例』で確認したとおり，日本語に対して一般的に用いられるtri-gramの計算アルゴリズムとpythonの実装ソースコードを記載する．
例文として「きしゃがきしゃにきしゃできしゃした(記者が貴社に汽車で帰社した)」を用いる．

<計算アルゴリズム>
①与えられた文章を3文字毎の記号列に分割する．
②分割後の文字列リストについて度数を計算
③相対度数を計算

# tri-gramの計算アルゴリズム
from collections import Counter
def culc_trigram(str):
	# ①与えられた文章を3文字ずつに分割
	split_str = [str[i:i+3] for i in range(0, len(str)-2, 1)]

	# ②分割後の文字列リストについて度数を計算
	trigram = dict(Counter(split_str))

	# ③相対度数を計算
	sum_freq = sum(trigram.values())
	trigram_rel = {}
	for k, v in trigram.items():
		trigram_rel.update({k : v / sum_freq})

	return trigram, trigram_rel

if __name__ == '__main__':
	# "きしゃがきしゃにきしゃできしゃした"のtrigramを計算
	trigram, trigram_rel = culc_trigram("きしゃがきしゃにきしゃできしゃした")
	print(trigram)
	#	{'きしゃ': 4, 'しゃが': 1, 'ゃがき': 1, 'がきし': 1, 'しゃに': 1, 'ゃにき': 1,
	#    'にきし': 1, 'しゃで': 1, 'ゃでき': 1, 'できし': 1, 'しゃし': 1, 'ゃした': 1}
	print(trigram_rel)
	#	{'きしゃ': 0.26666666666666666, 'しゃが': 0.06666666666666667, 'ゃがき': 0.06666666666666667,
	#    'がきし': 0.06666666666666667, 'しゃに': 0.06666666666666667, 'ゃにき': 0.06666666666666667,
	#    'にきし': 0.06666666666666667, 'しゃで': 0.06666666666666667, 'ゃでき': 0.06666666666666667,
	#    'できし': 0.06666666666666667, 'しゃし': 0.06666666666666667, 'ゃした': 0.06666666666666667}

# tri-gramの計算アルゴリズム

from collections import Counter

def culc_trigram(str):

# ①与えられた文章を3文字ずつに分割

split_str = [str[i:i+3] for i in range(0, len(str)-2, 1)]

# ②分割後の文字列リストについて度数を計算

trigram = dict(Counter(split_str))

# ③相対度数を計算

sum_freq = sum(trigram.values())

trigram_rel = {}

for k, v in trigram.items():

trigram_rel.update({k : v / sum_freq})

return trigram, trigram_rel

if __name__ == '__main__':

# "きしゃがきしゃにきしゃできしゃした"のtrigramを計算

trigram, trigram_rel = culc_trigram("きしゃがきしゃにきしゃできしゃした")

print(trigram)

# {'きしゃ': 4, 'しゃが': 1, 'ゃがき': 1, 'がきし': 1, 'しゃに': 1, 'ゃにき': 1,

# 'にきし': 1, 'しゃで': 1, 'ゃでき': 1, 'できし': 1, 'しゃし': 1, 'ゃした': 1}

print(trigram_rel)

# {'きしゃ': 0.26666666666666666, 'しゃが': 0.06666666666666667, 'ゃがき': 0.06666666666666667,

# 'がきし': 0.06666666666666667, 'しゃに': 0.06666666666666667, 'ゃにき': 0.06666666666666667,

# 'にきし': 0.06666666666666667, 'しゃで': 0.06666666666666667, 'ゃでき': 0.06666666666666667,

# 'できし': 0.06666666666666667, 'しゃし': 0.06666666666666667, 'ゃした': 0.06666666666666667}

ここまでの説明でN-gramについて理解できただろう．しかし，bi-gramマルコフモデルを理解するには，他にマルコフ連鎖を理解しなければならない．では，マルコフ連鎖とは何なのか，解説していこう．

マルコフ連鎖とは

マルコフ連鎖の概要

まず，wikipediaより引用した，マルコフ連鎖の定義を確認する．初めは意味が分からなくても構わないので，一度目を通してほしい．
“マルコフ連鎖（マルコフれんさ、英: Markov chain）とは、確率過程の一種であるマルコフ過程のうち、とりうる状態が離散的（有限または可算）なもの（離散状態マルコフ過程）をいう。また特に、時間が離散的なもの（時刻は添え字で表される）を指すことが多い（他に連続時間マルコフ過程というものもあり、これは時刻が連続である）。マルコフ連鎖は、未来の挙動が現在の値だけで決定され、過去の挙動と無関係である（マルコフ性）。各時刻において起こる状態変化（遷移または推移）に関して、マルコフ連鎖は遷移確率が過去の状態によらず、現在の状態のみによる系列である。” – マルコフ連鎖(wikipedia)

それでは，マルコフ連鎖を理解するため，まずは定義で用いられているマルコフ性について解説する．

マルコフ性とは

マルコフ性とは，確率論における確率過程の持つ特性の一種で，その過程の将来状態の条件付き確率分布が現在状態のみに依存し，過去のいかなる状態にも依存しない特性をもつことをいう．つまり，明日の天気は今日の天気にのみ左右される(昨日より前の天気は関係ない)ようなものである．
今回の解析対象である「単語」について考えると，ある単語が出現する確率は，直前の1単語にのみ左右されることになる．

確率過程をX(t)とし，時間t>0がマルコフ性をもつとすると，数学的に以下の式が成り立つ．
$$Pr[X(t+h)=y|X(s)=x(s),\forall s \leq t]=Pr[X(t+h)=y|X(t)=x(t)],\forall h>0$$

マルコフ性の解説は以上である．次に，同様に定義で用いられているマルコフ過程について解説する．

マルコフ過程とは

マルコフ過程とは，マルコフ性を持つ確率過程を指す．つまり，未来の挙動が現在の値(状態)のみで決定され，過去の挙動と無関係な性質を持つ確率過程のことである．
マルコフ過程にはいくつか種類があるが，今回は単純マルコフ過程と離散時間マルコフ過程に注目する．単純マルコフモデルを選んだ理由は後ほど説明するが，bi-gramマルコフモデルではこの単純マルコフモデルを採用しているからである．離散時間マルコフ過程を選んだ理由は，マルコフ過程の定義より“とりうる状態が離散的（有限または可算）なもの（離散状態マルコフ過程）をいう。また特に、時間が離散的なもの（時刻は添え字で表される）を指すことが多い。”からである．

それでは，先に単純マルコフ過程について解説しよう．

単純マルコフ過程とは

単純マルコフ過程は単にマルコフ過程と呼ばれることもあり，定義は『マルコフ過程とは』の項に記載した内容と同一である．『マルコフ性とは』の項で用いた天気の例では明日の天気は今日の天気にのみ依存していたが，これこそまさしく単純マルコフ過程を指していたのである．

では，次に離散時間マルコフ過程について解説しよう．

離散時間マルコフ過程とは

離散時間と名のつく通り，時間が離散的に変化するマルコフ過程である．通常は，T={1,2,3…}を時間の集合とする．

マルコフ過程について理解したところで，本題に戻ってマルコフ連鎖の定義を再度確認しよう．

マルコフ連鎖とは(再確認)

マルコフ連鎖の定義を再確認しよう．
“マルコフ連鎖（マルコフれんさ、英: Markov chain）とは、確率過程の一種であるマルコフ過程のうち、とりうる状態が離散的（有限または可算）なもの（離散状態マルコフ過程）をいう。また特に、時間が離散的なもの（時刻は添え字で表される）を指すことが多い（他に連続時間マルコフ過程というものもあり、これは時刻が連続である）。マルコフ連鎖は、未来の挙動が現在の値だけで決定され、過去の挙動と無関係である（マルコフ性）。各時刻において起こる状態変化（遷移または推移）に関して、マルコフ連鎖は遷移確率が過去の状態によらず、現在の状態のみによる系列である。” – マルコフ連鎖(wikipedia)
ここまでのマルコフ過程や離散時刻マルコフ過程の解説を通して，最初に読んだ時よりは定義を理解できることを期待したい．
それでは，最後にbi-gramマルコフモデルについて解説しよう．あと少しなので，頑張って読み進めてほしい．

bi-gramマルコフモデルとは

bi-gramマルコフモデルの概要

bi-gramマルコフモデルとはあるタイミングの単語の生起(出現)確率は直前の1単語にのみ依存すると仮定したモデルであり，これは単純マルコフ過程を指す．N-gramに拡張した場合，あるタイミングの単語の生起(出現)確率は，直前のN-1単語にのみ依存すると定義し，N-1重マルコフ過程に従うことを表す．

bi-gramマルコフモデルので使用される式

『bi-gramマルコフモデルの概要』で紹介した『あるタイミングの単語の生起(出現)確率は，直前の1単語にのみ依存すると仮定したモデル』を数学的に表すと，以下の定義が得られる．
ある単語列W=w₁,w₂,…w_nが与えられたとき，単語列をW，コーパス内の単語の生起確率をCとすると，同時生起確率P(W)は以下の式で定義される．
$$P(W)=\prod_{i=1}^{n} P(w_i|w_{i-1}) = \prod_{i=1}^{n} \left(\frac{C(w_i,w_{i-1})}{C(w_{i-1})}\right)$$

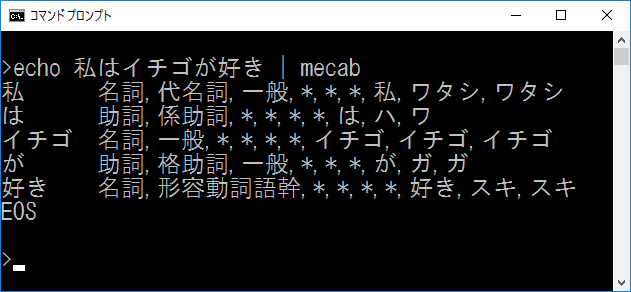
例として，「私はイチゴが好き」という単語列の同時生起確率Pを表す式は以下のようになる．

ここで*BOS*は文章の開始を，*EOS*は文章の終わりを表す，文章には出現しない単語とする．*BOS*，*EOS*の生起確率は1である(文章の開始と終了は必ず存在するため)．また，各単語の生起確率は，コーパス内での各単語の度数/全単語数で計算する．

bi-gramマルコフモデルの計算例(とpythonでの実装例紹介)

bi-gramマルコフモデルのアルゴリズムと計算例
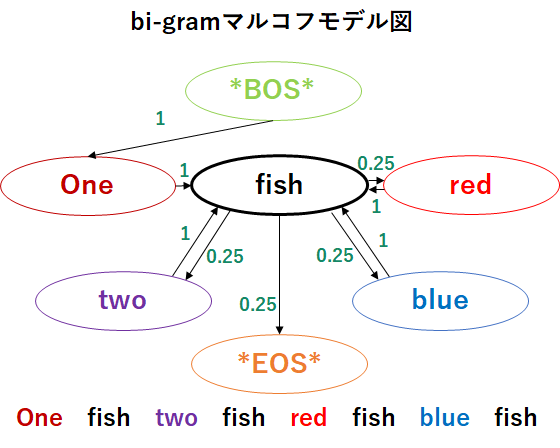
例として，「One fish two fish red fish blue fish」という単語列のみが与えられた際のマルコフモデルを考えよう．bi-gramマルコフモデルは以下の手順で作成する．
①単語列の先頭と末尾に*BOS*，*EOS*を付加する．
②それぞれの単語について，その単語の次に出現する単語とのペアを作成する．
③各ペアについて，その選択肢が選ばれる確率についての情報を付与する．

上記の例から作成したbi-gramマルコフモデル図は以下のようになる．

bi-gramマルコフモデルのpythonでの実装例紹介

bi-gramマルコフモデルをpythonで実装する場合，以下のサイトが大変わかりやすい．
[元サイト]
From “What is a Markov Model” to “Here is how Markov Models Work”
[日本語訳サイト]
マルコフモデル～概要から原理まで～（前編）
マルコフモデル～概要から原理まで～（後編）
このサイトでは前編で「マルコフモデルとは何か」を解説し，後編で「pythonでの実装例」を紹介している．マルコフモデルについて更に知識を深めたい場合は，参照することをお勧めする．

bi-gram(N-gram)マルコフモデルの応用例(形態素解析，音声認識)

今回紹介したbi-gram(N-gram)マルコフモデルは，様々な分野で応用されている．最後に，いくつかの応用例を紹介しよう．

bi-gramマルコフモデルの応用例(形態素解析)

代表的な形態素解析器であるMeCabやJUMANでは，解析モデルにbi-gramマルコフモデルを採用している．これにより，未知語に対して品詞情報を推定できるようになる等，より柔軟に解析ができるようになった．

bi-gramマルコフモデルの応用例(音声認識)

音声認識分野ではある言葉を読み取った際に「次にくる言葉は何か」を判断する際に，bi-gram(N-gram)マルコフモデルを使用する場合がある．一般に，音声認識システムから受け取った言語データに対して適用される．

参考

【書籍】
・金明哲:テキストデータの統計科学入門(2009)．
・北研二:言語と計算ー４　確率的言語モデル(1999)．

【Webサイト】
・マルコフ性 – wikipedia
・マルコフモデル～概要から原理まで～（前編）
・マルコフモデル～概要から原理まで～（後編）
・n-gram言語モデル
・Ngram言語モデルメモ
・1.マルコフモデルとは
・マルコフ連鎖と日本語形態素解析によるワードサラダSEO

人工知能・機械学習・自然言語処理周辺の技術情報