執筆:金子冴
今回は,形態素解析器の1つであるMeCab内で学習モデルとして用いられているCRF(Conditional random field)について解説する.
初めに,CRFのwikipediaの定義を確認しよう.
CRF(Conditional random field)の定義
“条件付き確率場(じょうけんつきかくりつば、英語: Conditional random field、略称: CRF)は無向グラフにより表現される確率的グラフィカルモデルの一つであり、識別モデルである。” – 条件付き確率場(wikipedia)
また,CRFは特徴的に訓練されたマルコフ確率場(マルコフ性のある確率変数の集合)である.
それでは,定義に登場する用語について無向グラフから順に解説する.
無向グラフとは
無向グラフは方向性のないエッジ(辺)とノード(頂点)からなるグラフである.方向性がないとは,両方向に行き来できるという意味である.例えば,ノードni(i=1,2,3,4)とエッジej(j=1,2,3,4)からなる無向グラフは以下のようになる.
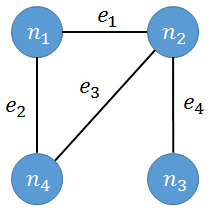
無向グラフについては問題ないだろう.
次に,確率的グラフィカルモデルについて解説する.
確率的グラフィカルモデルとは
確率的グラフィカルモデルとは,グラフが確率変数間の条件付き依存関係を示すような確率モデルを指す.確率的グラフィカルモデルのノードは確率変数を表し,エッジは依存関係を表す.
確率的グラフィカルモデルを考えるメリットには,以下のようなことが挙げられる.
●簡単に確率モデルを視覚化できるため,設計に役立つ
●条件付き独立性などの性質がわかりやすい
●推論や学習の計算をグラフ上の操作として表現できる
代表的な確率的グラフィカルモデルには,マルコフ確率場(Markov Random Field):無向グラフィカルモデルやベイジアンネットワーク(Bayesian Network):有向グラフィカルモデルが挙げられる.
最後に,識別モデルについて解説する.
識別モデルとは
識別モデルとはあるデータxがクラスCkに属する確率p(Ck|x1)を表すモデルを指す.
例えば,クラスC1に属するデータx1が入力されたときに
p(C1|x1) = 0.92
p(C2|x1) = 0.07
p(C3|x1) = 0.01
となり,データx1がクラスC1に属する確率p(Ck|x)を表したモデルを指す. 識別モデルを使用した場合,推定の結果を確率で得ることができる.上記の例でいえば,データx1がクラスC1に属する確率は92%,クラスC2に属する確率は7%,クラスC3に属する確率は1%という推定結果となる.
推定結果を確率で受け取ることで,クラスの境界面付近での分布の推定が可能となる. 識別モデルの最も基本的なものに,CRFでも採用されている対数線形モデル(log-linear model)(最大エントロピーモデルとも呼ばれる)がある.
それでは,機械学習におけるCRFの立ち位置を解説しよう.
機械学習におけるCRF(Conditional random field)の立ち位置
CRFは系列ラベリングという問題を解くために用いられる手法である.では,系列ラベリングとはどういう問題なのだろうか.まずは機械学習における最も基本的な問題である分類問題と,CRFで解くような系列ラベリング,そしてCRFで用いられている手法である構造学習について簡単に解説しよう.
機械学習における問題(分類問題,系列ラベリング)
機械学習の最も基本的な問題は分類問題であろう.例えば届いたメールがスパムメールかどうか,入力されたデータがどのクラスに属しているか等を判断するような問題が挙げられる.分類問題では与えられる入力データは1つの場合が多く,そのデータをどのクラスに分類するかを判別することが目的となる.
これに対して系列ラベリングは,入力にデータ列(例えば単語列)を受け取り,出力として個々のデータにラベルを付加することが目的となる.例えば単語列に品詞情報を与える問題(入力:「私/は/走る」⇒出力:「名詞/助詞/動詞」)などが挙げられる.
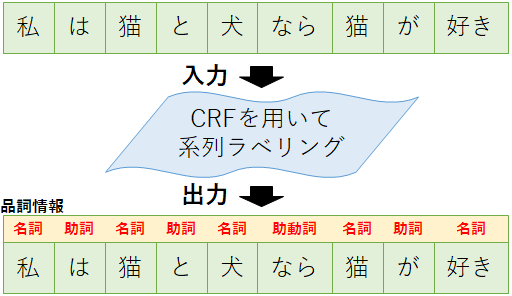
系列ラベリングを解くためのCRFを,特にLinear-chain CRFと呼ぶ.以降,CRFと表記している場合はLinear-chain CRFを指していると考えてほしい.
機械学習における手法(構造学習)
系列ラベリングについては,ご理解いただけただろうか. 実は,系列ラベリングの入力であるデータ列を個々のデータに分割して入力とすることで,系列ラベリングを分類問題として解くこともできる.上記の例であれば,まず「私」の品詞を分類問題で解き,次に「は」の品詞を分類問題で解き,次に「猫」の品詞を…と繰り返すことで,すべてのデータに対してラベリングすることが可能である.しかし,個々のデータで見たときには最適な分類をしたものの,結果として全体では最適でない結果となってしまうこともある.
例として,「My face is like a dog(私の顔は犬のようです)」という英文を日本語訳する問題を考えてみよう.個々の単語に分けてからそれぞれを日本語訳すると,「My(私の)」「face(顔)」「is(です)」「like(好き)」「a(冠詞のため訳なし)」「dog(犬)」となり,それぞれ問題ないように見える.しかし全体で見ると「like」を好きと訳してしまったために文中の動詞が2つとなってしまい,文法に反する文章と判別されてしまう.CRFではこのような問題を解決し,全体で最適な結果を得るため,構造学習という手法を取り入れている.構造学習を取り入れることで,私の顔を犬のようにできるかもしれない.
構造学習とは,系列ラベリングを解く際に入力であるデータ列を個々のデータに分割して入力とせず,まとめてデータ列を渡してデータごとのラベルを得る手法である.上記の日本語訳の例では「like」の意味を推定する際にその単語のみを用いていた.構造学習では,周辺の情報(文法や,次の単語の情報等)も取り入れて分類する.上記の例でいえば,すでに動詞(「is」)が出現していることや三人称単数形(「likes」)でないことなどから,「like」を「~のよう」と想定通りに日本語訳(分類)することができるようになる.
では,これまでの説明を踏まえて,CRFの定義式を確認していこう.
CRFの定義式
あるCRFを考えよう.前述のとおり本解説ではLinear-chain CRFを対象とするため,モデルのノードは線形に接続されている. 観測された入力系列をO(o1,o2,…,oT)とする.また,出力系列をS(s1,s2,…,sT)とする.
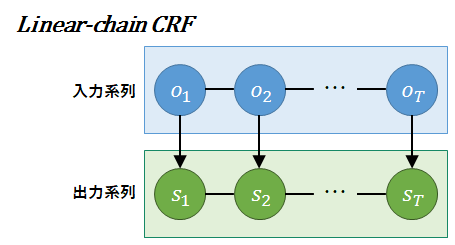
CRFで求める条件付き確率は以下の式で定義される.
それでは,定義式の各項について説明する.
CRFの目的関数の項(fk(st-1,st,o,t))
関数fkは,素性関数である.素性関数を理解するため,まずは素性について説明しよう.
素性(そせい)とは入力系列の特徴を指す.素性の値を素性値と呼ぶ.機械学習における特徴,特徴量と同じようなものと考えるとよい.CRFでは遷移素性と観測素性の二種類が用いられる.また,素性値をベクトル化したものを素性ベクトルと呼ぶ. では,次に素性関数を説明しよう.
素性関数とはある素性について条件が一致した場合に1を返し,それ以外の場合は0を返す関数を組み合わせ,素性ベクトルを返す関数である.CRFで利用する素性関数は周辺情報を利用する遷移素性と周辺情報を利用しない観測素性の2種類で表現される.遷移素性と観測素性について解説する.
遷移素性(bi-gram feature)とは,周辺情報を利用する素性である.例えば「名詞の次なら助詞」や「助詞の次なら動詞」が遷移素性にあたる.もっと広い範囲の周辺情報を利用すれば今より正確にラベリングが可能になる気がするが,『CRF(Conditional random field)の定義』の項にも記載したとおり,CRFはマルコフ確率場上に成り立っているため,現在の状態は1つ前の状態にのみ依存する.したがって,1つ前の状態以前の状態と現在の状態は独立といえるため,広い範囲の周辺情報を利用する必要がないと判断できる.
観測素性(uni-gram feature)とは,周辺情報を利用しない素性である.例えば「名詞で”私”が観測される」や「動詞で”走る”が観測される」が観測素性にあたる.この時,観測の可否はモデル作成に使用したコーパスに出現しているかに依存する.
素性関数の例
遷移素性と観測素性について確認できたところで,素性関数の例を挙げよう.前述のとおり,素性関数は遷移素性と観測素性を組み合わせ,条件が一致した場合に1を返す関数である.「名詞の次に助詞が出現し(遷移素性),かつ助詞で”が”が観測される(観測素性)」という素性関数は以下のように表現される.
このような素性関数を複数用意することで,その文章の素性(特徴)ベクトルを作成する. 一般的に文章の特徴を1つずつ人力で見つけ出すのは時間がかかるため,素性テンプレート等を用いて素性関数を作成する.素性テンプレートについては以下のスライドの解説が大変わかりやすい. Crfと素性テンプレート
以上が,素性関数の説明である.では,素性ベクトルの作成例を確認しよう.
素性関数の作成例
入力系列Oを「私/は/友人/の/犬/と/公園/を/走る」とする.MeCabを用いて品詞情報を確認すると,「名詞/助詞/名詞/助詞/名詞/助詞/名詞/助詞/動詞」という出力が得られた.ここで,品詞区分を「名詞(N)」,「助詞(P)」,「動詞(V)」と与えると,出力系列は「N-P-N-P-N-P-N-P-V」と表せる. それではまず,無向グラフを作成してみよう.以下の図が,作成した無向グラフである.
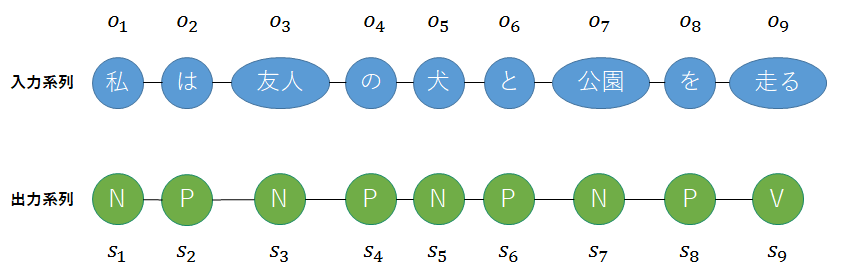
次に,以下のような素性関数を定義する.
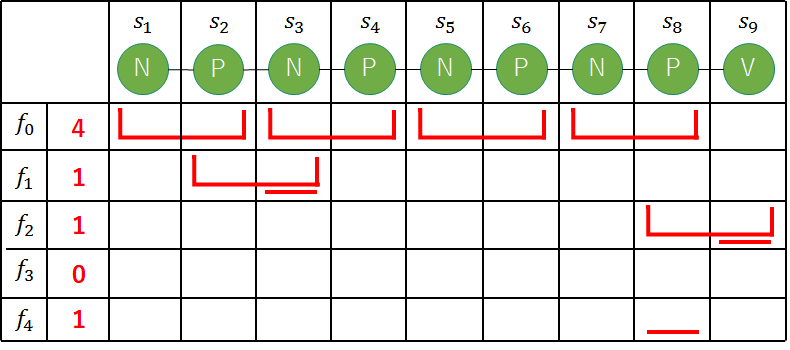
それでは,素性ベクトルf[f0,f1,f2,f3,f4]を考えよう.ここで,素性ベクトルの各要素はすべての素性関数を適用した場合の素性値の合計であることに注意すること.
①1要素目f0は,t=2,4,6,8の時に成り立つため,素性値の合計は4となる.
⇒f[4,f1,f2,f3,f4]
②2要素目f1は,t=3の時のみ成り立つため,素性値の合計は1となる.
⇒f[4,1,f2,f3,f4]
③3要素目f2は,t=9の時のみ成り立つため,素性値の合計は1となる.
⇒f[4,1,1,f3,f4]
④4要素目f3は,どのtでも成り立たないため素性値の合計は0となる.
⇒f[4,1,1,0,f4]
⑤5要素目f4は,t=8の時のみ成り立つため素性値の合計は1となる.
⇒f[4,1,1,0,1]
よって,素性ベクトルはf[4,1,1,0,1]となる.
次は,素数ベクトルの各要素に対して重みを付ける重みλk について確認しよう.
CRFの目的関数の項(λk)
λkは,前述のとおり素性ベクトルの各要素に対する重みである.CRFでは,この重みλkを最適化することで精度を向上させていく. 重みの具体的な役割を確認しよう.『素性関数とは』の項でも確認した通り,素性値は0か1である.しかし,より特徴を捉えている素性については重視する必要がある.そこで,素性ベクトルの各要素(素性値)と重み(重要度)をかけ合わせることで,コストを計算する.重みλkの値は-∞~+∞の間で設定される.後続の記事で解説するViterbiアルゴリズムでは経路ごとのコストを元に解を探索するため,この重みをどのように設定するかがとても重要となる.一般的に,重みは最急降下法等の最適化手法を用いて最適化する(最適化手法については別記事として掲載する予定のため,ここでは説明を割愛する).
『素性関数の作成例』の項で用いた例で,どのような場合に重みを大きく(もしくは小さく)するのか説明しよう. 例で挙げた素性関数では「名詞の次が助詞」(f0)が成り立つ場合も,「助詞の次に名詞”友人”を観測」(f1)が成り立つ場合も同様に素性値として1を返す.しかし,多種多様な系列に対して品詞情報を付加した場合,前者の素性が成り立つ文章はかなり多く,後者の素性が成り立つ文章は少ないと推測できる.そのような場合,前者の素性が出現した際はその経路が合っている確率(可能性)が高いと判断できるため,重みλ0の値を大きくする.逆に,後者の素性が出現しても,それだけではその経路が合っているか判断しづらいため,重みλ1の値を小さくする. 重みλkについて理解出来ただろうか.最後に,Zoの項について確認する.
CRFの目的関数の項(Zo)
Zoは,全経路のスコアの合計を表す.全経路のスコアの合計で選択された経路のスコアを割ることで,入力Oを与えたときに出力Sが得られる確率を得ることができる.このように,ある値を0~1の範囲に収めることを正規化といい,正規化のための項Zoを正規化項と呼ぶ.
CRF(Conditional random field)の応用例(形態素解析,物体認識)
CRFの応用例(形態素解析)
今回の解説でも例で挙げたように,CRFは形態素解析の学習モデルとして用いられる.形態素解析器であるMeCabの学習モデルもCRFで構築されている.
CRFの応用例(物体認識)
画像の領域に対して「人」「道路」「空」等のラベリングをする等の問題にて,位置関係を考慮したラベリングを行うためにCRFが用いられる.TextonBoostという画像認識手法では,Semantic Image Segmentationという手法によってラベリングされたデータに対してCRFを適用することで,画像全体の最適化を行っている.
参考
【論文】
・Efficiently Inducing Features of Conditional Random Fields
・言語処理における識別モデルの発展 – HMMからCRFまで
【書籍】
・奥村 学,高村 大也:言語処理のための機械学習入門(2010).
【Webサイト】
・有向および無向グラフ
・グラフィカルモデル入門
・グラフィカルモデルによる確率モデル設計の基本
・識別関数、識別モデル、生成モデルの違いを解説
・CRFがよくわからなくてお腹が痛くなってしまう人のための30分でわかるCRFのはなし
・今さら聞けない人工知能の仕組み(1) 機械学習は「素性」で男女を見分ける
・間違ってるかもしれないCRFの説明
・隠れマルコフモデル(HMM)と条件付き確率場(CRF)
・CRFについて
・最大エントロピーモデル(対数線形モデル)について
・領域分割(3) – CRFを用いたSemantic Image Segmentation
・日本語形態素解析の裏側を覗く!MeCab はどのように形態素解析しているか

