執筆:金子冴
今回はマルコフモデルと,マルコフモデルを拡張した隠れマルコフモデルを題材に,それぞれのモデルの解説と2つのモデルの違いについて解説する.
まずはマルコフモデルについて解説しよう.
目次
マルコフ過程とは
マルコフ過程の分類とマルコフ連鎖について
隠れマルコフモデルとは
マルコフモデルと隠れマルコフモデルの違い(応用例)
参考
マルコフ過程とは
マルコフモデルを説明すると言っておきながら,見出しがマルコフ過程となっていることに疑問を抱く人もいるだろう.一般的にマルコフモデルといった場合,マルコフ過程を指す.それでは,マルコフモデル改め,マルコフ過程の概要を確認しよう.
マルコフ過程の概要
“マルコフ過程(マルコフかてい)とは、マルコフ性をもつ確率過程のことをいう。すなわち、未来の挙動が現在の値だけで決定され、過去の挙動と無関係であるという性質を持つ確率過程である。” – マルコフ過程(wikipedia)
上記の概要にある確率過程とマルコフ性については,定義を確認する必要があるだろう.初めに確率過程について確認する.
確率過程とは
確率過程とは何を指すのだろうか.まずはwikipediaを確認しよう.
“確率論において、確率過程(かくりつかてい、英語: stochastic process)は、時間とともに変化する確率変数のことである。 株価や為替の変動、ブラウン運動などの粒子のランダムな運動を数学的に記述する模型(モデル)として利用している。不規則過程(英語: random process)とも言う。” – 確率過程(wikipedia)
wikipediaの言葉を借りれば,確率過程とは時間と共に変化する確率変数を指すらしい.では確率変数とは何なのか.
wikipediaによると,確率変数とはランダムな実験により得られ得る全ての結果を指す変数との記述がされていた.私たちがよく使う確率は一義的に値が決まるのとは違い,確率変数は確率に従って定義域内の様々な値を取ることができる.簡単に言い直すと,確率変数は確率を決めるときに利用する数である.
例を挙げて確率変数を理解しよう.
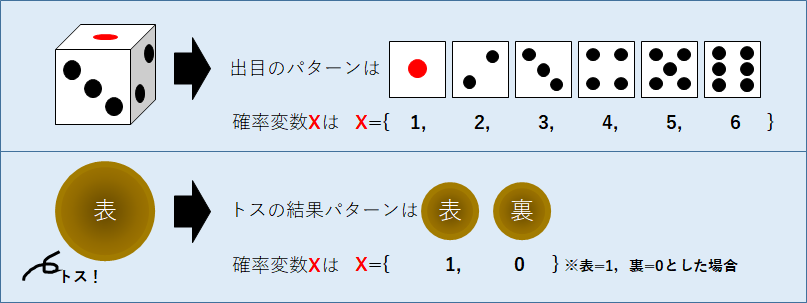
確率変数の例としてよく使われるのはサイコロである.今回は,1から6の目がある6面体のサイコロを考える.この時,出目の取りうる値,つまり確率変数XはX={1,2,3,4,5,6}と表される.他にもコイントスの例を考えてみると,コイントスの結果は「表」「裏」の2択のため,「表=1」「裏=0」と定義した場合,確率変数XはX={1,0}と表せる.
では,確率過程の説明に戻ろう.
定義では,確率過程とは時間と共に変化する確率変数となっていた.先ほど挙げたサイコロやコインの例は,この確率過程に当てはまらないことはわかるだろう.なぜなら,サイコロの目やコインの表裏は時間と共に変化しないからである.ここでいう「時間と共に変化」とは,サイコロを振って出目を確認した後,その1秒後にもう一度見たら出目が変わっているようなことを指す.
確率過程について,例を挙げてみよう.
確率過程の例には,株価の変動が挙げられる.ここで,株価が500円以上の確率が0.4,500円未満の確率が0.6である状況を仮定しよう.この場合,確率はある時点での株価によって決まるが,株価は時間と共に刻一刻と変わっていくため,時間によって確率は変動する.このように時間で変化する確率変数を確率過程と呼ぶ.

確率過程についてはご理解いただけただろうか.ここで,確率過程の定義には出現していないが,確率分布についても解説しておこう.確率分布は,その次に解説するマルコフ性の定義に出現しているため事前に理解しておく必要がある.
確率分布とは
確率分布のwikipediaを確認すると,以下のように説明されている.
“確率分布(かくりつぶんぷ, 英: probability distribution)は、確率変数の各々の値に対して、その起こりやすさを記述するものである。” – 確率分布(wikipedia)
確率分布には確率変数が離散的な場合と確率変数が連続的な場合が存在するが,ここでは離散的な場合を考える.連続的な場合を理解するためには測度の概念等が必要となるため,ここでは割愛する.
理想的な6面サイコロを考えてみよう.ここでいう理想的とはすべての出目(つまり確率変数)の出る確率が同じことを指す.サイコロには6面存在し,すべての出目が出る確率が同じ場合,各出目の出る確率は1/6となるため,X={1,2,3,4,5,6}とした時,確率分布PXは以下のようになる.
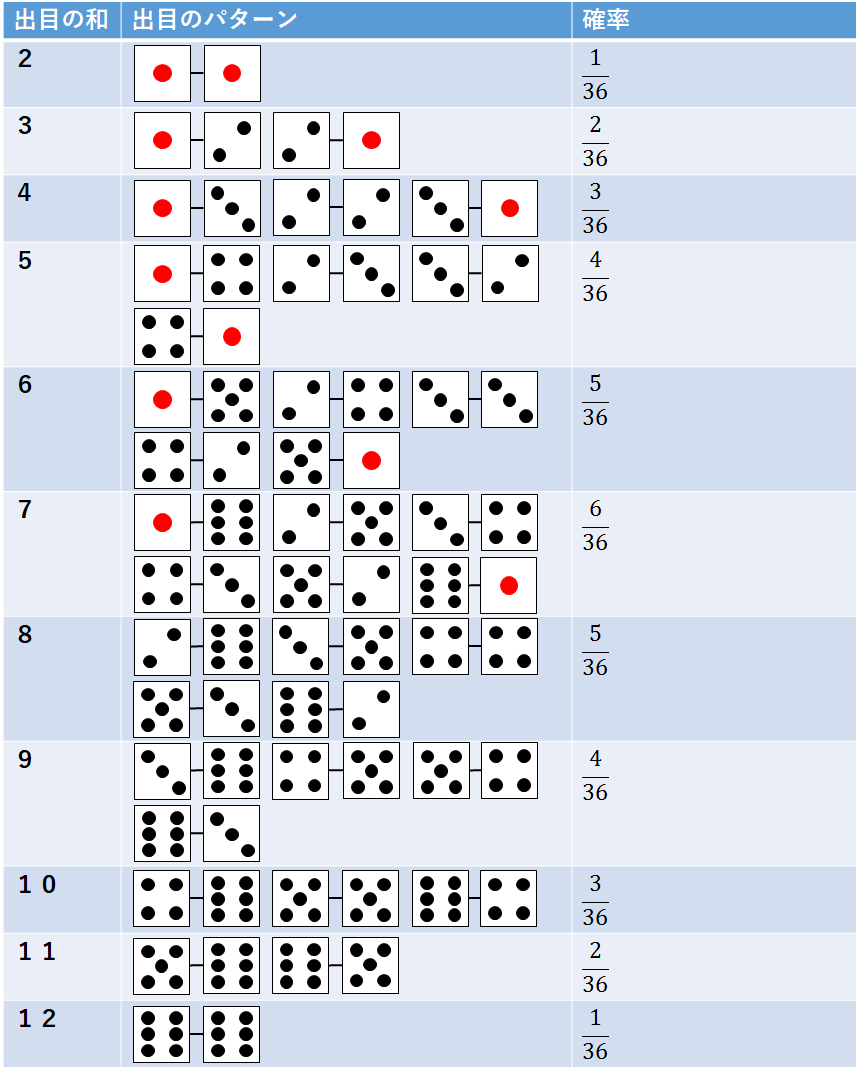
少し難しい例として,理想的な6面サイコロを2回投げた時の出目の和の確率分布を考えてみよう.
出目の和と出目のパターン,その確率は以下の図のようになる.このときの確率の分布を表したものが確率分布となり,確率変数が離散的な場合にはヒストグラムで表されることが多い.
併せて,条件付き確率分布についても簡単に確認しておこう.
条件付き確率分布とは
条件付き確率分布とは事象が2つ存在する場合に一方の事象が発生した場合の,もう一方の事象が発生する確率の分布を指す.
事象Aと事象Bについて,事象Aが発生したときの事象Bの条件付き確率P(B|A)は以下の式で定義される.
この条件付き確率の分布を表したものが,条件付き確率分布である.
確率分布,条件付き確率分布についても理解できたところで,次はマルコフ性について確認しよう.
マルコフ性とは
マルコフ性について,wikipediaで定義を確認しよう.
“マルコフ性(マルコフせい、英: Markov property)とは、確率論における確率過程の持つ特性の一種で、その過程の将来状態の条件付き確率分布が、現在状態のみに依存し、過去のいかなる状態にも依存しない特性を持つことをいう。すなわち、過去の状態が与えられたとき、現在の状態(過程の経路)は条件付き独立である。” – マルコフ性(wikipedia)
確率過程X(t)についてt>0がマルコフ性を持つとき,数学的に以下の式が成り立つ.
この式からわかる通り,X(t+h)の確率分布はs<tとなるすべてのsの事後確率ではなく,直前(t)のみの事後確率として定義される.
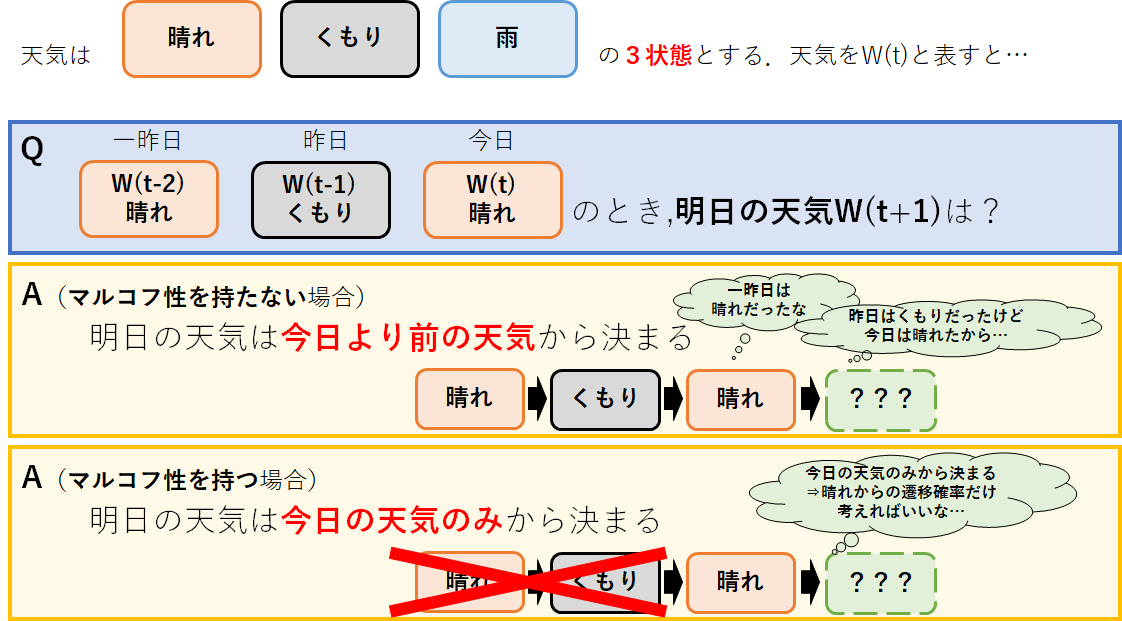
例えば,天気がマルコフ性を持つ場合を仮定してみよう.
一般的に,翌日の天気は今日までの雲の動きを参考に予測される.つまり,翌日の天気を予測するためには,昨日以前の天気の情報も利用する必要がある.しかし,天気がマルコフ性を持つ場合,明日の天気は今日の天気にのみ左右される(昨日より前の天気は関係ない)ため,昨日以前の天気の情報を利用する必要がなくなる.
マルコフ性について理解できただろうか.
それでは,これまでの知識からマルコフ過程のまとめをしよう.
マルコフ過程のまとめ
『マルコフ過程の概要』の項で確認した通り,マルコフ過程はマルコフ性をもつ確率過程のことをいう.マルコフ性は将来(次の)状態の条件つき確率分布は現在状態のみに依存する性質を指し,確率過程は時間と共に変化する確率変数を指す.
マルコフ過程(マルコフモデル)については理解できただろうか.2つ目の大きな題材である隠れマルコフモデルについて解説する前に,マルコフ過程の分類について確認したい.そうすることで,隠れマルコフモデルがより理解しやすくなるためである.
それでは,マルコフ過程の分類とマルコフ連鎖について解説しよう.
マルコフ過程の分類とマルコフ連鎖について
まずは,マルコフ過程の分類について確認しよう.
マルコフ過程の分類
マルコフ過程は以下の7つに分類される.
◆単純マルコフ過程
現在状態のみから将来状態が決定されるマルコフ過程のこと.単にマルコフ過程と呼ぶ場合は,この単純マルコフ過程を指している場合が多い.
◆N階(N重)マルコフ過程
連続したN個の状態から将来状態が決定されるマルコフ過程のこと.N=1のとき,単純マルコフ過程を指す.また,N個の状態を現在状態と定義しなおすことにより,単純マルコフ過程として表現することも可能である.
◆離散時間マルコフ過程
時刻tが離散的な場合のマルコフ過程のこと.一般的に時刻の集合はT={1,2,3,…}と定義する.
◆連続時間マルコフ過程
離散時間マルコフ過程と違い,時刻tが連続的な場合のマルコフ過程のこと.時刻の集合をT=[0,∞)等と定義する.
◆離散マルコフ過程
マルコフ過程の状態空間が離散集合であるマルコフ過程のこと.つまり,状態が離散的でありマルコフ性が成り立つようなマルコフ過程を指す.
◆連続マルコフ過程
離散マルコフ過程と違い,マルコフ過程の状態空間が連続的であるマルコフ過程のこと.
◆時間的に一様なマルコフ過程
状態の推移確率が時間に依らず一定であるようなマルコフ過程のこと.
では,この分類を元にマルコフ連鎖の概要をwikipediaで確認しよう.
マルコフ連鎖の概要
“マルコフ連鎖(マルコフれんさ、英: Markov chain)とは、確率過程の一種であるマルコフ過程のうち、とりうる状態が離散的(有限または可算)なもの(離散状態マルコフ過程)をいう。また特に、時間が離散的なもの(時刻は添え字で表される)を指すことが多い(他に連続時間マルコフ過程というものもあり、これは時刻が連続である)。マルコフ連鎖は、未来の挙動が現在の値だけで決定され、過去の挙動と無関係である(マルコフ性)。各時刻において起こる状態変化(遷移または推移)に関して、マルコフ連鎖は遷移確率が過去の状態によらず、現在の状態のみによる系列である。” – マルコフ連鎖(wikipedia)
概要にもある通り,マルコフ連鎖とはマルコフ過程のうち状態が離散,かつ時間が離散なものを指す場合が多い.分類では離散時間マルコフ過程,離散マルコフ過程に該当するマルコフ過程がマルコフ連鎖に該当する.
次にマルコフ連鎖の定義について確認する.
マルコフ連鎖の定義
マルコフ連鎖の定義は,マルコフ性の定義とよく似ている.違うのは時刻が離散的であることより,時刻を添え字で表している点である.
ここで,確率変数Xiの取りうる値は連鎖の状態空間と呼ばれる.マルコフ連鎖は有向グラフで表され,グラフの各ノードは確率変数,エッジはノード間の遷移確率を表す.
ここで,代表的なマルコフ連鎖である単純マルコフ連鎖とN階マルコフ連鎖について確認しよう.
単純マルコフ連鎖とN階マルコフ連鎖
ここでいう単純とは,将来状態が現在状態のみから決まることを指す.つまり『マルコフ連鎖の定義』の項で紹介した定義式こそ,単純マルコフ連鎖を表す式である.
対してN階とは,将来状態が現在状態を含むN個の状態から決まることを指す.その場合,定義式は以下のようになる.
単純マルコフ連鎖について,少し掘り下げて理解していこう.
例として,マルコフ連鎖上で成り立つ天気が以下の状態遷移図で表される場合を考える.ここで,各ノードは天気,エッジはある天気からある天気への遷移確率とする.例えば,以下の図でいえば「晴れ」からそれぞれの天気に遷移する確率は,「晴れ」が50%,「曇り」が約33%,「雨」が約16%となる.
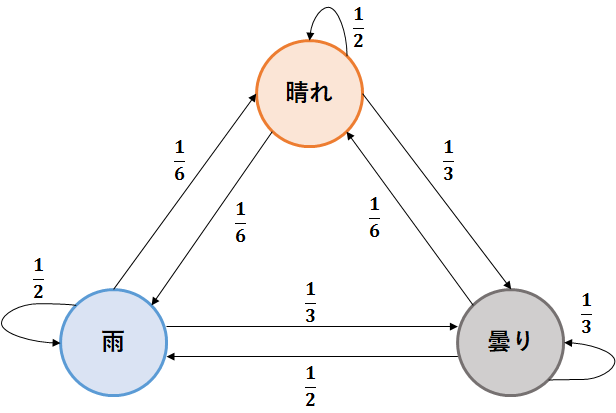
この状態遷移を行列W(Weatherの頭文字)として表現すると以下のようになる.
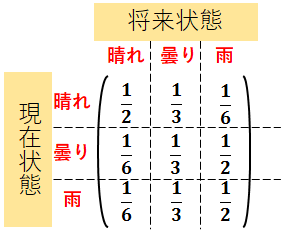
あるタイミングtでの天気をwtT=(x1,x2,x3)と表現するとしよう.ここで,x1は晴れの確率,x2は曇りの確率,x3は雨の確率とする.上付き文字のTは転置を表しているため,実際のwtは3行1列の行列である.
現在観測できている時刻tの天気が晴れの場合,wtT=(1,0,0)となる.
次の時刻t+1の天気wt+1が知りたいときは,状態遷移行列Wと現在の天気wtをかけ合わせることで求められる.
つまり,wt+1=W・wt=(1/2,1/6,1/6)となるため,次の日が「晴れ」の確率が50%,「曇り」の確率が約16%,「雨」の確率が約16%であるとわかる.
次に,時刻t+2の天気が知りたいときは,状態遷移行列Wと時刻t+1の天気wt+1をかけ合わせればよい.
つまり,wt+2=W・wt+1=W・W・wt=(1/3,2/9,2/9)となる.
ここから,初期状態の天気をw0とすると,ある時刻tの天気はwt+n=Wn・wtで計算できることがわかる.
上記のWnをt→∞として求めると,状態遷移の定常分布を求めることができる.定常分布とは,無限回遷移した場合にそれぞれの状態にたどり着く確率のことを指す.ここでは計算を割愛するが,今回の例で定常分布を求めると,無限回遷移したときにそれぞれの天気になる確率がわかる.このように,単純マルコフ連鎖の定常分布は状態遷移を行列に表すことで容易に計算することが可能となる.
単純マルコフ連鎖については理解いただけただろうか.それでは,本題の隠れマルコフモデルについて解説しよう.
隠れマルコフモデルとは
名前からわかる通り,マルコフモデルとは違い隠れマルコフモデルは何かが隠れているのだろうと推測できる.では,何が隠れているのだろうか?
ではいつも通り,まずは隠れマルコフモデルの定義を確認しよう.
隠れマルコフモデル(Hidden Markov Model;HMM)の概要
“隠れマルコフモデル(かくれマルコフモデル、英語: Hidden Markov Model)は確率モデルのひとつであり、観測されない(隠れた)状態をもつマルコフ過程である。” – 隠れマルコフモデル(wikipedia)
単純マルコフ連鎖では状態が直接観測可能であったため,状態の遷移確率のみをパラメータとしていた.一方,隠れマルコフモデルにおいては状態が直接観測されず,出力のみが観測される.ここで確認しておきたいのは,「状態」と「出力」の違いである.先ほどまで用いていた天気の例では,「状態(=晴れ,曇り,雨)」がそのまま「出力」となっているため,隠れマルコフモデルの説明には適さない.ここでは,新たに例を挙げて,隠れマルコフモデルについて確認しよう.
あるところに散歩が好きな一人暮らしのマルコフ少年と,マルコフ少年の母のマルコフ母がおり,2人が住む場所はとても遠いと仮定する.マルコフ少年は自分の住んでいる街の天気を元に,散歩をどうするか(「長距離」,「短距離」,「散歩なし」)を決めており,その結果のみを毎日マルコフ母に電話している.なお,マルコフ少年が散歩する確率は,マルコフ少年の住む街の天気によって以下のように決定する.
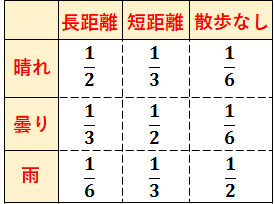
また,マルコフ少年の住む街の天気は以下のように状態遷移するとしよう.

このとき,マルコフ母はマルコフ少年が住む街の天気(状態)を知ることができないため,隠れた状態となっている.しかし,マルコフ少年の散歩の結果(出力)は知ることができる.このようなモデルのことを,隠れマルコフモデルと呼ぶ.
隠れマルコフモデルでは,パラメータとして遷移確率と出力確率の2種類をとる.遷移確率とは,状態から状態に遷移する確率を表し,上記の例でいえば天気の状態遷移確率がこれに当たる.出力確率とは,ある状態で出力が得られる確率を表し,上記の例でいえば「晴れの時に長距離散歩する確率」や「雨の時に散歩しない確率」がこれに当たる.
隠れマルコフモデルから可能な推定
隠れマルコフモデルから推定可能なものとその際に使用するアルゴリズムを紹介する.
「状態」の推定
最も想像しやすいのは,隠れマルコフモデルで隠されている「状態」の推定であろう.今回の例でいえば,マルコフ少年が住む街の天気の状態遷移確率,天気と散歩の関係(確率),マルコフ少年が報告した散歩の結果から,マルコフ母がマルコフ少年の住む街の天気を推測する.
その際にはビタビアルゴリズムという動的計画法の一種であるアルゴリズムが使用され,取りうる状態のパターンから最も尤もらしいパターンを選び出すことができる.
パラメータ(遷移確率と出力確率)の推定
隠れマルコフモデルでは,「出力」から遷移確率と出力確率を推定することも可能である.その際にはバウム=ウェルチアルゴリズムというフォワードバックワードアルゴリズムの一種であるアルゴリズムが採用され,主に音声や遺伝子などの系列データを解析するために使用される.
最後に,マルコフモデルと隠れマルコフモデルの違いについて,応用例をもとに確認しよう.
マルコフモデルと隠れマルコフモデルの違い(応用例)
マルコフモデルの応用例
マルコフモデルは,天気予報や証券の取引の場面に応用されている.天気予報の分野では,例に挙げた通り状態遷移行列を用いてn日後の天気wt+nが推測できることを確認した.また,定常分布を計算して求めることで,限りなく未来の天気について,それぞれの天気になる確率を求めることができる.
また,Googleで使用されている,ウェブページの重要度を決定するアルゴリズムであるPageRankでもマルコフモデルが使用されている.これも天気と同様にユーザが各ページに遷移する確率から定常分布を求めることで,最後にユーザが開いているページを推測し,重要度を決めている.
このように,マルコフモデルでは「状態」と「出力」が判明しているため,状態遷移行列から無限遷移後の存在確率を求めることが可能である.
隠れマルコフモデルの応用例
マルコフモデルと隠れマルコフモデルの違いといえば,「状態」が隠れているかいないかであろう.では,「状態」が隠れていることのメリットは何なのだろうか.実際には,「状態」が隠れていることではなく状態が推測できるというメリットの方が大きい.隠れマルコフモデルを使用する分野の一つに音声認識分野がある.音声信号に対して隠れマルコフモデルを当てはめ,音声認識や音声合成に応用されている.例えば,音声認識では与えられた音声から任意の単語列を推測する際に隠れマルコフモデルが使用されている.それにより,個人差が生まれやすい「発声法」等の音声パターンの変動を確率モデルで捉えることができ,数学的,統計的に処理することが可能となる.
参考
【書籍】
・金 明哲:テキストデータの統計科学入門(2009).
・北 研二:言語と計算ー4 確率的言語モデル(1999).
【Webサイト】
・マルコフ過程 – wikipedia
・確率過程 – wikipedia
・確率分布 – wikipedia
・条件付き確率 – wikipedia
・マルコフ性 – wikipedia
・隠れマルコフモデル – wikipedia
・マルコフ連鎖の話
・マルコフ連鎖モンテカルロ法入門-1
・隠れマルコフモデルの大雑把な解説
・隠れマルコフモデルによる音声認識と音声合成

