今回は潜在意味解析(Latent Semantic Analysis: LSA)を確率的に発展させたトピックモデルの確率的潜在意味解析(PLSA)について解説します.
このモデルを使うと潜在的な意味をトピックとして抽出でき,そのトピック内で単語と文書が出現する確率がわかります.主に既存のデータの分析に用いられています.
目次
確率的潜在意味解析(PLSA)とは
PLSAのアルゴリズム
PLSAの学習
EMアルゴリズム (E-step)
EMアルゴリズム (M-step)
過学習の対策 (TEM)
LSAとPLSAの比較
PLSAでの分析例
PLSAの応用
PLSAの問題点
参考文献
確率的潜在意味解析(PLSA)とは
確率的潜在意味解析(Probabilistic Latent Semantic Analysis: PLSA)とは,1999年にHofmannらが発表したトピックモデルの代表例である.トピックモデルは,文書は複数の独立した潜在的なトピックから成るものとして,その過程を確率分布を用いてあらわした確率モデルである.
例えば,「車中泊」についての文章は「自動車」や「キャンプ」などのトピックからなると考えられる.「自動車」から単語「車」,「車内」,「座席」が生成され,「キャンプ」から単語「泊まる」,「水」,「自炊」,「寝る」が生成されたとする.その場合「車中泊」についての記事の単語群(BOW)は{車, 車内, 座席, 泊まる, 水, 自炊}となる.トピックモデルでは一般的に語順は考慮されない.この場合に生成される文書の例として「車に泊まるとき,車内で自炊ができるように水を持っていくとよいでしょう.また車内で寝られるよう座席がフルフラットにできる車を選びましょう.」があげられる.実際には「動詞」や「助詞」を表すトピックもここには入っている.
トピックモデルを用いる場合,文章を生成することよりもその単語や文書がどのトピックから生成されたのかに焦点を当てることの方が多い.そのため,先ほど例に挙げた文書を解析し,トピック「自動車」や「キャンプ」などを得たり,トピック「自動車」において「車」や「座席」はどれほど影響を与えるのかなどについて分析を行う.
PLSAのアルゴリズム
PLSAのアルゴリズムを解説していく.
用いる記号
単語:$W = \{w_1,w_2,…,w_M\}$
文書:$D = \{d_1,d_2,…,d_N\}$
トピック:$Z = \{z_1,z_2,…,z_K\}$
単語と文書の同時確率
$$
\displaystyle
\begin{eqnarray}
P(D, W) &=& P(D)P(W|D) \\
&=& P(D)\sum_{k=1}^{K}P(W|z_k)P(z_k|D) \\
&=& P(D)\sum_{k=1}^{K}P(W|z_k)\frac{P(D|z_k)P(z_k)}{P(D)} \\
&=& \sum_{k=1}^{K}P(W|z_k)P(D|z_k)P(z_k)
\end{eqnarray}
$$
途中,$P(z_k|D)$に対してベイズの定理を用いて$P(D)$を消去している.
最終的にはトピック$Z$から単語$W$と文章$D$が生成されることと等価になる.
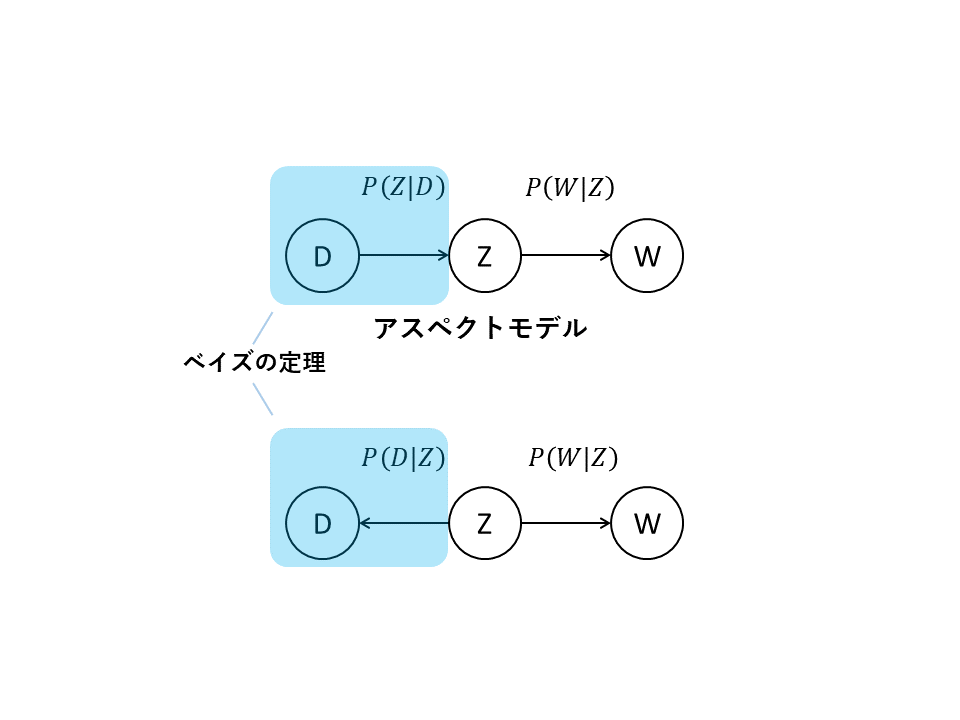
これのモデルはアスペクトモデルと呼ばれる.
PLSAの学習
対数尤度
$$
\displaystyle
\begin{eqnarray}
L &=& \sum_{i=1}^{M}\sum_{j=1}^{N}n(d_j,w_i)\log P(d_j,w_i) \\
&=& \sum_{i=1}^{M}\sum_{j=1}^{N}n(d_j,w_i)\log \sum_{k=1}^{K}P(w_i|z_k)P(d_j|z_k)P(z_k) \\
&=& \sum_{i=1}^{M}\sum_{j=1}^{N}n(d_j,w_i)\log \sum_{k=1}^{K}P(z_k|d_j,w_i)\frac{P(w_i|z_k)P(d_j|z_k)P(z_k)}{P(z_k|d_j,w_i)}
\end{eqnarray}
$$
$n(d_j,w_i)$は文書$d_j$で単語$w_i$が出現する回数を表す.
また,EMアルゴリズムでは潜在変数(トピック)$z_k$の事後分布を,上記のようにくくり出す準備をする.
対数尤度の下限
上記の対数尤度に対して,イェンセンの方程式を用いて下限を求める.
logの中にΣがある形は解析的に求めることが困難なので,イェンセンの方程式を用いてΣをlogの外に出している.
また,対数尤度の下限を最大化するパラメータを求めることにより,間接的に対数尤度を最大化する.
$$
\displaystyle
\begin{eqnarray}
L &\geq & \sum_{i=1}^{M}\sum_{j=1}^{N}\sum_{k=1}^{K}n(d_j,w_i)P(z_k|d_j,w_i)\log (\frac{P(w_i|z_k)P(d_j|z_k)P(z_k)}{P(z_k|d_j,w_i)}) \\
&= & \sum_{i=1}^{M}\sum_{j=1}^{N}\sum_{k=1}^{K}n(d_j,w_i)P(z_k|d_j,w_i)\log (P(w_i|z_k)P(d_j|z_k)P(z_k)) \\
& & – \sum_{i=1}^{M}\sum_{j=1}^{N}\sum_{k=1}^{K}n(d_j,w_i)P(z_k|d_j,w_i)\log (P(z_k|d_j,w_i))
\end{eqnarray}
$$
トピック$z$の事後分布からなる2項目を固定し(E-step),その他の事後分布を求める.(M-step)
これを繰り返し,対数尤度が収束するまで行う.
EMアルゴリズム (E-step)
トピック$z$の事後分布を求める.
$$
\displaystyle
\begin{eqnarray}
P(Z|D,W) &=& \frac{P(D,W,Z)}{P(D,W)} \\
&=& \frac{P(Z)P(W|Z)P(D|Z)}{\sum_{k=1}^{K}P(z_k)P(W|z_k)P(D|z_k)} \\
\end{eqnarray}
$$
EMアルゴリズム (M-step)
トピック$z$の事後分布を固定した状態で,その他の事後分布を求める.
対数尤度$L$に対してラグランジュの未定乗数法を用いる.
$$
\displaystyle
\begin{eqnarray}
F &= & \sum_{i=1}^{M}\sum_{j=1}^{N}\sum_{k=1}^{K}n(d_j,w_i)P(z_k|d_j,w_i)\log (P(w_i|z_k)P(d_j|z_k)P(z_k)) \\
& & + \lambda_1(1-\sum_{i=1}^{M}P(w_i|z_k))+ \lambda_2(1-\sum_{j=1}^{N}P(d_j|z_k))+ \lambda_3(1-\sum_{k=1}^{K}P(z_k))
\end{eqnarray}
$$
$P(w_i|z_k)$を求める (M-step)
$$
\displaystyle
\begin{eqnarray}
\frac{\delta F}{\delta P(w_i|z_k)} &= & \frac{\sum_{j=1}^{N}n(d_j,w_i)P(z_k|d_j,w_i)}{P(w_i|z_k)} – \lambda_1 = 0 \\
\end{eqnarray}
$$
ゆえに,
$$
\displaystyle
\begin{eqnarray}
P(w_i|z_k) = \frac{\sum_{j=1}^{N}n(d_j,w_i)P(z_k|d_j,w_i)}{\lambda_1}
\end{eqnarray}
$$
ここで両辺の$\sum_{i=1}^{M}$をとる.
$$
\displaystyle
\begin{eqnarray}
\lambda_1 = \sum_{i=1}^{M}\sum_{j=1}^{N}n(d_j,w_i)P(z_k|d_j,w_i)
\end{eqnarray}
$$
これを代入して,
$$
\displaystyle
\begin{eqnarray}
P(w_i|z_k) = \frac{\sum_{j=1}^{N}n(d_j,w_i)P(z_k|d_j,w_i)}{\sum_{i^{\prime}=1}^{M}\sum_{j=1}^{N}n(d_j,w_{i^{\prime}})P(z_k|d_j,w_{i^{\prime}})}
\end{eqnarray}
$$
$P(d_j|z_k)$を求める (M-step)
$$
\displaystyle
\begin{eqnarray}
\frac{\delta F}{\delta P(d_j|z_k)} &= & \frac{\sum_{i=1}^{M}n(d_j,w_i)P(z_k|d_j,w_i)}{P(d_j|z_k)} – \lambda_2 = 0 \\
\end{eqnarray}
$$
ゆえに,
$$
\displaystyle
\begin{eqnarray}
P(d_j|z_k) = \frac{\sum_{i=1}^{M}n(d_j,w_i)P(z_k|d_j,w_i)}{\lambda_2}
\end{eqnarray}
$$
ここで両辺の$\sum_{j=1}^{N}$をとる.
$$
\displaystyle
\begin{eqnarray}
\lambda_2 = \sum_{i=1}^{M}\sum_{j=1}^{N}n(d_j,w_i)P(z_k|d_j,w_i)
\end{eqnarray}
$$
これを代入して,
$$
\displaystyle
\begin{eqnarray}
P(d_j|z_k) = \frac{\sum_{i=1}^{M}n(d_j,w_i)P(z_k|d_j,w_i)}{\sum_{i=1}^{M}\sum_{j^{\prime}=1}^{N}n(d_{j^{\prime}},w_i)P(z_k|d_{j^{\prime}},w_i)}
\end{eqnarray}
$$
$P(z_k)$を求める (M-step)
$$
\displaystyle
\begin{eqnarray}
\frac{\delta F}{\delta P(z_k)} &= & \frac{\sum_{i=1}^{M}\sum_{j=1}^{N}n(d_j,w_i)P(z_k|d_j,w_i)}{P(z_k)} – \lambda_3 = 0 \\
\end{eqnarray}
$$
ゆえに,
$$
\displaystyle
\begin{eqnarray}
P(z_k) = \frac{\sum_{i=1}^{M}\sum_{j=1}^{N}n(d_j,w_i)P(z_k|d_j,w_i)}{\lambda_3}
\end{eqnarray}
$$
ここで両辺の$\sum_{k=1}^{K}$をとる.
$$
\displaystyle
\begin{eqnarray}
\lambda_3 = \sum_{i=1}^{M}\sum_{j=1}^{N}\sum_{k=1}^{K}n(d_j,w_i)P(z_k|d_j,w_i)
\end{eqnarray}
$$
これを代入して,
$$
\displaystyle
\begin{eqnarray}
P(z_k) &= & \frac{\sum_{i=1}^{M}\sum_{j=1}^{N}n(d_j,w_i)P(z_k|d_j,w_i)}{\sum_{i=1}^{M}\sum_{j=1}^{N}\sum_{k^{\prime}=1}^{K}n(d_j,w_i)P(z_{k^{\prime}}|d_j,w_i)} \\
&= & \frac{\sum_{i=1}^{M}\sum_{j=1}^{N}n(d_j,w_i)P(z_k|d_j,w_i)}{\sum_{i=1}^{M}\sum_{j=1}^{N}n(d_j,w_i)}
\end{eqnarray}
$$
過学習の対策 (TEM)
EMアルゴリズムを用いた混合分布の学習において,過剰適合(過学習)を防ぐためにアニーリング法のTEM(Tempered EM)が用いられる.
TEMのアルゴリズム
EMアルゴリズムのEステップにおけるトピック$z$の事後分布を,パラメータ(inverse computational temperature)$β$を用いて以下のように定義する.
$$
\displaystyle
\begin{eqnarray}
P(Z|D,W) &=& \frac{P(Z)\bigl[ P(W|Z)P(D|Z)\bigr] ^β}{\sum_{k=1}^{K}P(z_k)\bigl[ P(W|z_k)P(D|z_k)\bigr] ^β} \\
\end{eqnarray}
$$
$β<1$の範囲での尤度を割り引く.
$β=1$から徐々に温度をさげていき,尤度が収束するまでEステップとMステップを繰り返す.
LSAとPLSAの比較
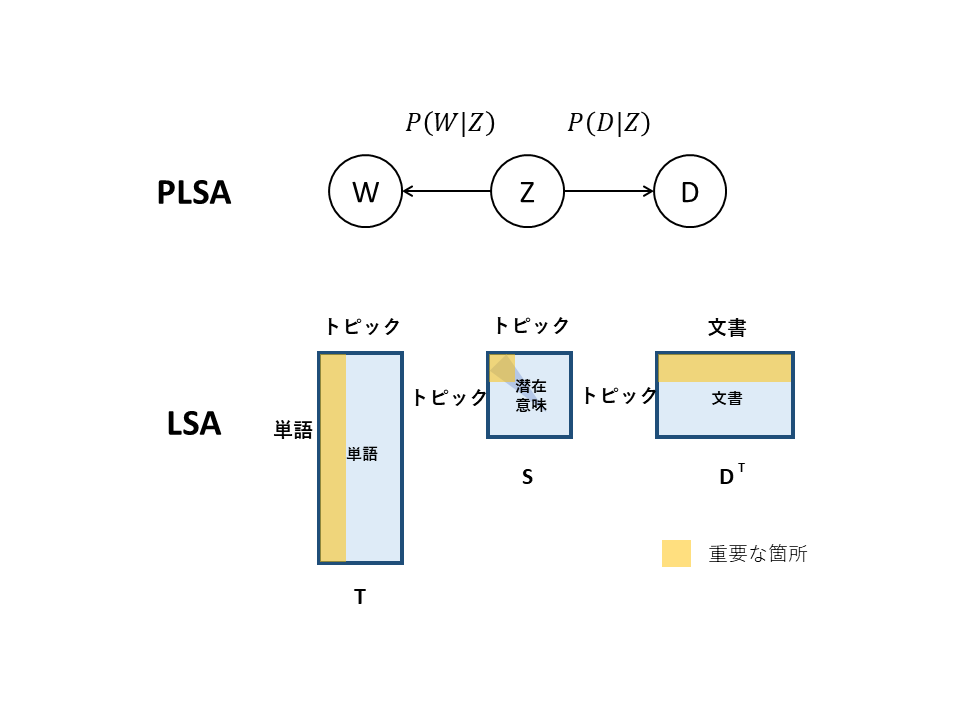
PLSAはLSAを確率モデルとして発展させたモデルである.
PLSAでは単語も文章も複数のトピックから確率的に生成される.
PLSAにおける各トピック間には独立性を仮定するため,トピック間の類似度は求められない.
PLSAでの分析例
「車中泊」についての記事を集めて生成した文書にPLSAを適用してみた.
以下,各トピックに対する事後分布の大きい順に示す.
単語-トピック
トピック1: 場,駅,道,全国,寝泊り
トピック2: 車中,泊,車,子供,トイレ
トピック3: 場合,ドライバー,周囲,一般,目
文章-トピック
(※ 本来文章の集合が出てくるが,今回はスペースの都合上その性質のみを記す.)
トピック1: 場所に関する文章が集まった
トピック2: メリット・デメリット,快適に過ごすための方法に関する文章が集まった
トピック3: 法律や注意事項,ルールに関する記事が集まった
解釈してみる
PLSAではトピックは人間が解釈しなくてはならないが,単語や文章とトピックの関係に着目してみるとなんとなくそれが何を表しているかがわかる.
トピック1では「車中泊をする場所」を,トピック2では「車内に泊まる時のこと」を,トピック3では「周囲の状況」を表していると解釈できる.
今回はWeb上の記事から取ってきた文章をもとに解析を行った.そのため,車中泊についてのサイトでは泊まる場所や快適に過ごすための方法,法律やルールについて書かれていることが分かった.
また,それぞれのトピックにおいて注目すべきキーワードもわかった.
PLSAの応用
共起性に着目すれば,文書と単語以外のものについても同様の分析ができる.
PLSAでは,何らかの2つのエンティティの共起行列から,その潜在クラス分析や,クラスとエンティティとの関係を求めることができる.
例えば,文書の分類や,単語の分類などはもちろん,ユーザーとその属性から似たようなユーザーを求めるといったリコメンドエンジンにも使うことができる.
応用例
・ID-POS分析
・協調フィルタリングの実装
・リコメンドエンジン
・要因分析
PLSAの問題点
・トピック間に独立性を仮定しているため,それらの関係を無視している
・新たなデータの追加に弱い
参考文献
【論文】
T. Hofmann, 1999, Probabilistic latent semantic indexing, Proceedings of Proceeding UAI’99 Proceedings of the Fifteenth conference on Uncertainty in artificial intelligence, p289-296.
【本】
岩田具治, 2015, トピックモデル, 講談社.



